Предмет: Геометрия,
автор: znanija22228
20 баллов, пошагово, с рисунком
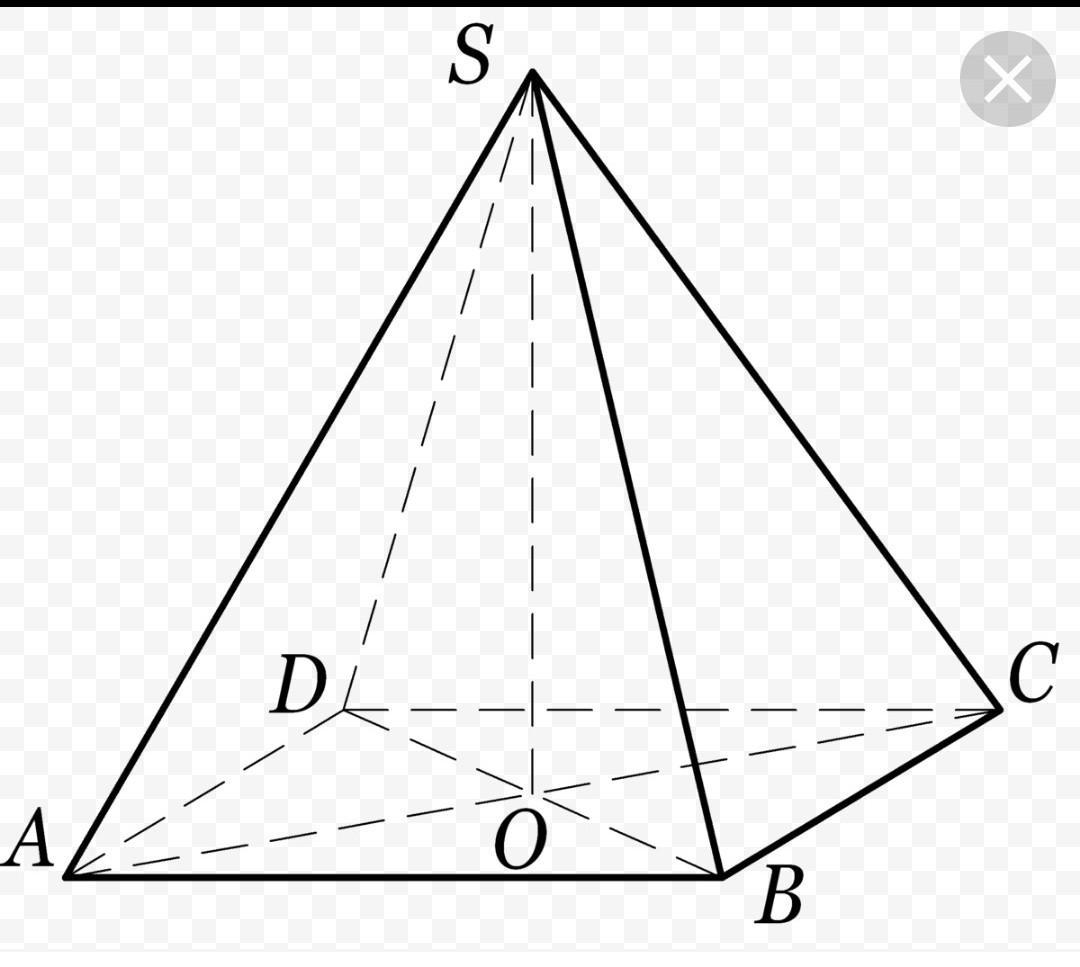
B правильной четырехугольной пирамиде сторона основания 8 см. Высота пирамиды 7 см. Вычислить боковое ребро пирамиды.
В ответе должно получиться 9 см.
Ответы
Автор ответа:
1
Ответ:
найдем диагонал основания
так как основания квадрать диагонал будет
вычислим ребро с помощью теорема пифагора
ответ 9
здесь С ребро
d диагонал основания
h высота
Автор ответа:
1
Ответ:
АВ=8=a
SO=7
ищем SB
в основании квадрат со стороной 8
диагональ DB= a√2=8√2
диагонали точкой пересечения делятся пополам, OA=OB=OC=OD=4√2
Теорема Пифагора для треугольника OSB
SB=√(SO²+OB²)=√49+16×2=√81=9
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: jack747
Предмет: Алгебра,
автор: polonskaangelina
Предмет: Английский язык,
автор: Driuchenko
Предмет: Математика,
автор: kutuzovaolgam
Предмет: Математика,
автор: 7882ka