Предмет: Алгебра,
автор: dtopoleva
Сравните корни пожалуйста, с решением.. я знаю, что корень из 36 больше , но как это обьяснить..
Приложения:
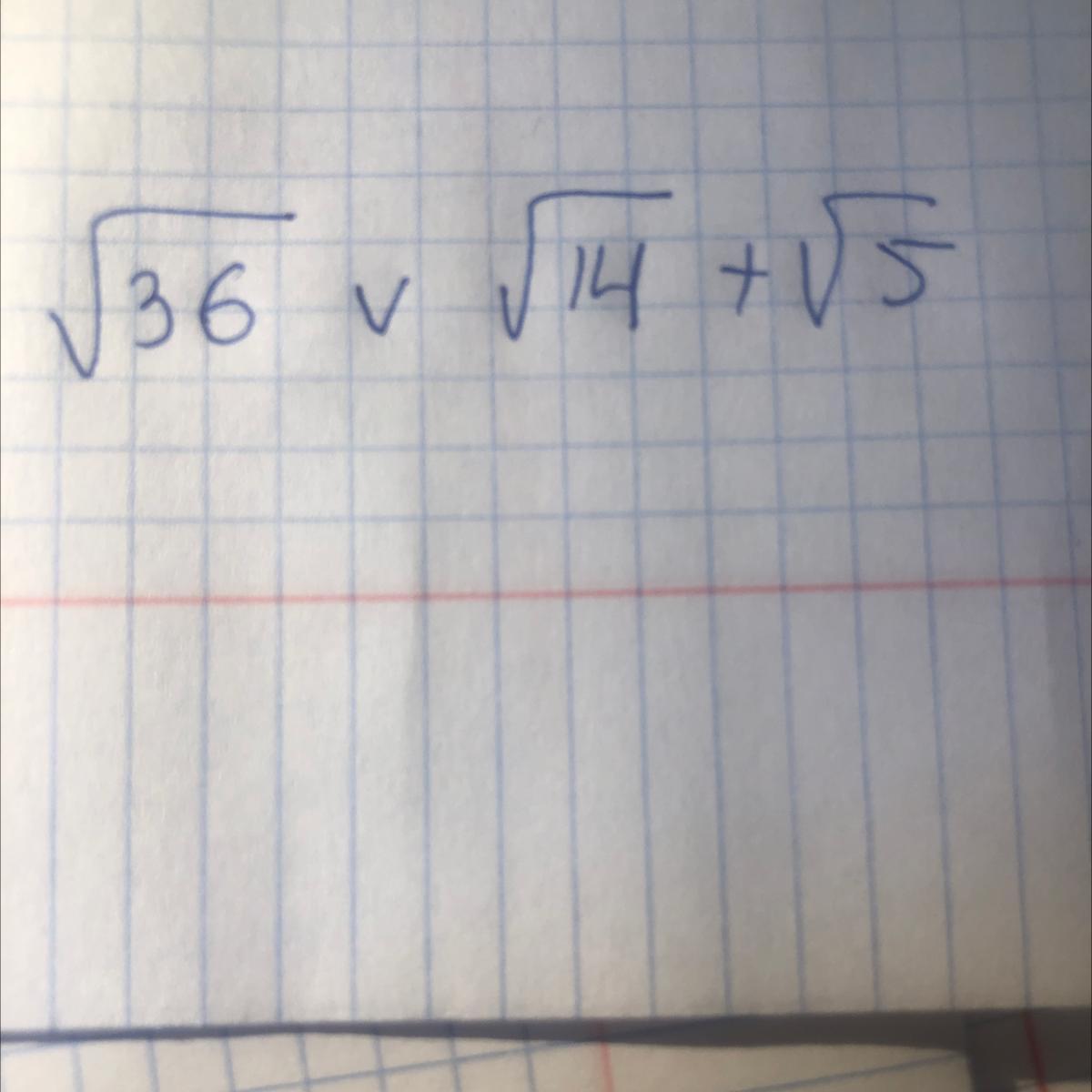
Ответы
Автор ответа:
1
Ответ:
Если , то
.
Похожие вопросы
Предмет: Русский язык,
автор: eficviktoriya
Предмет: Другие предметы,
автор: kseniaperm79
Предмет: Физика,
автор: 66611
Предмет: Информатика,
автор: JenyaPivovar
Предмет: Алгебра,
автор: Dascha852