Предмет: Математика,
автор: aviationtheory
Нужно решить 2 из 5 любых диф. уравнения из списка.
Ставлю максимальный бал. Помогите, пожалуйста.
Если что-то непонятно по цифрам и тд, то спрашивайте. Отвечу сразу!
Помогите, пожалуйста!
Приложения:
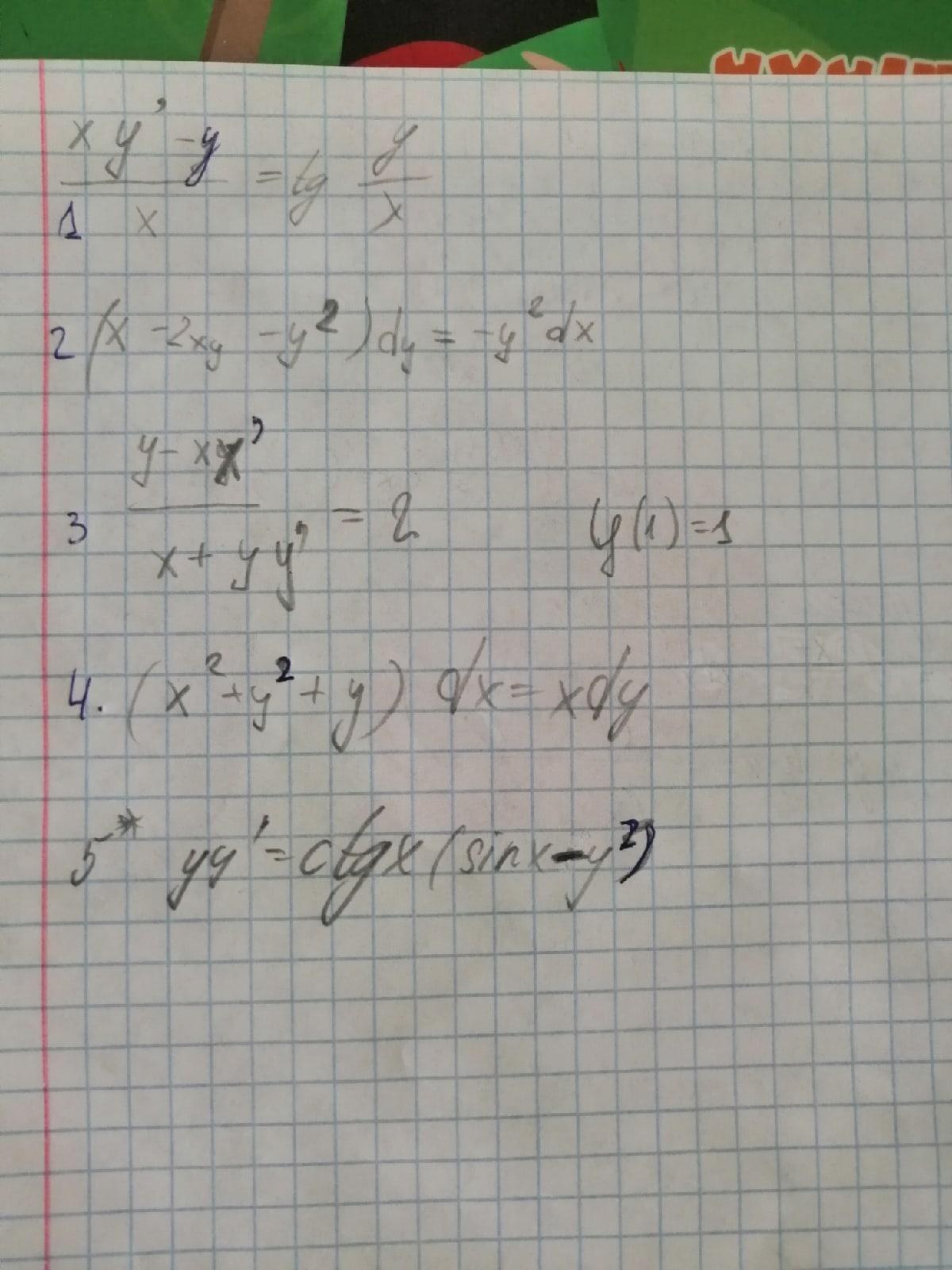
Ответы
Автор ответа:
0
Ответ:
1.
однородное ДУ
Замена:
константу можно представить в любом виде, для удобства преобразования пишу lnC
общее решение
4.
однородное ДУ
Замена:
общее решение
aviationtheory:
СПАСИБО БОЛЬШОЕ!!!!
Похожие вопросы
Предмет: Химия,
автор: christinajewell
Предмет: Физика,
автор: Гайка11
Предмет: Физика,
автор: Heymedinger
Предмет: Математика,
автор: gcvbhuj234
Предмет: Русский язык,
автор: eminzeynalov2