Предмет: Математика,
автор: pastetrylit123
Помогите сделать не могу!!!
Приложения:
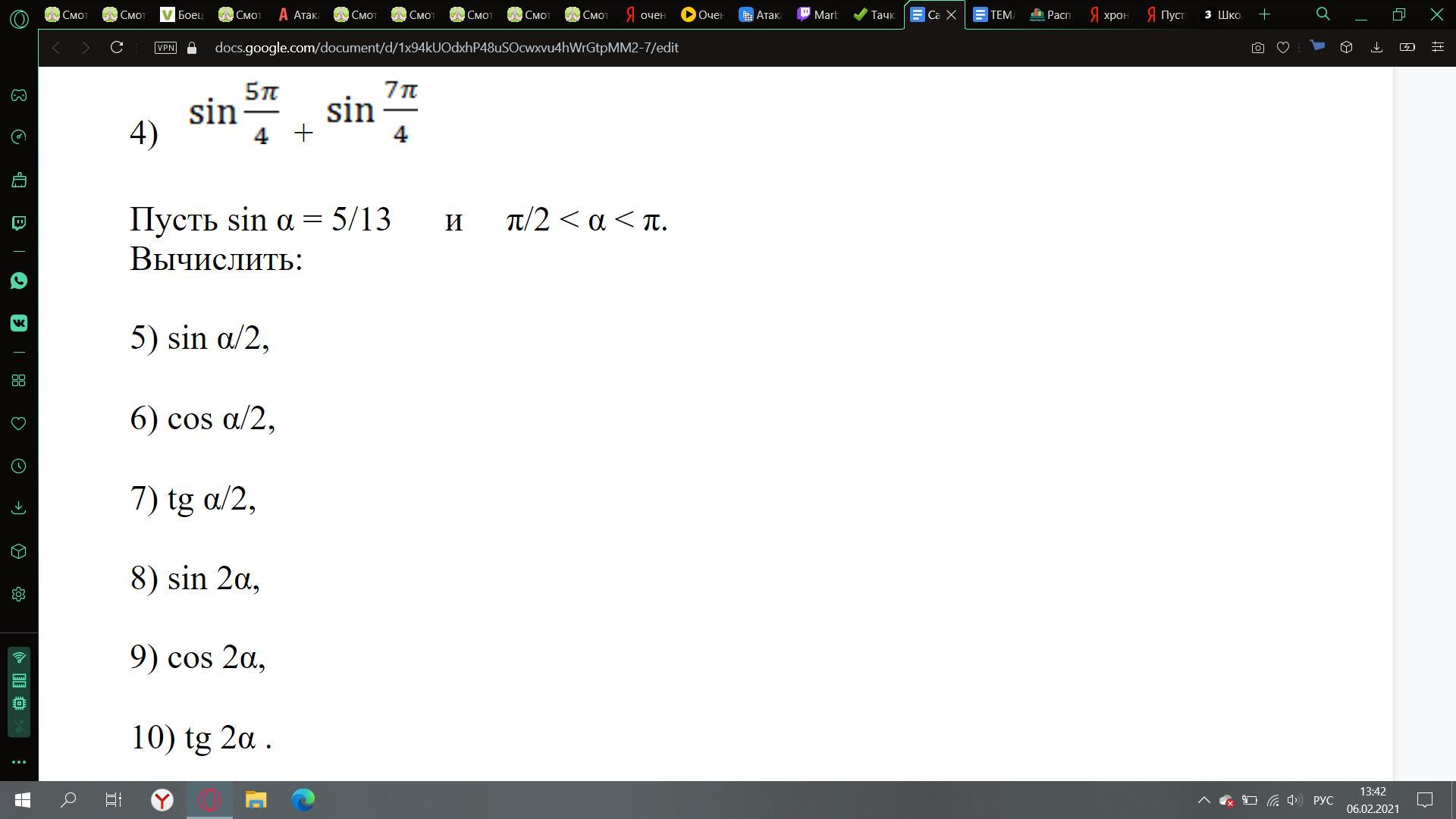
Ответы
Автор ответа:
0
Ответ:
4
5
угол принадлежит 2 четверти, косинус отрицательный
Похожие вопросы
Предмет: Биология,
автор: KOCMOHABT
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: DRUNKBURAT
Предмет: История,
автор: AXMED2001
Предмет: Геометрия,
автор: Kot2134342