Предмет: Математика,
автор: vleonov86vl
Найти производную функции
Приложения:
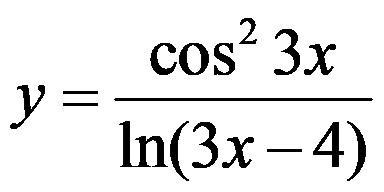
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Физика,
автор: kalaneka
Предмет: Физика,
автор: дайза
Предмет: Физика,
автор: kalaneka
Предмет: Литература,
автор: manydiamond