Предмет: Алгебра,
автор: CaTBaT
Сколько корней имеет уравнение
(sin^2 x + sinx) cosx =0
На промежутке [0 4П]
Ответы
Автор ответа:
0
Решение во вложении.))))
Приложения:
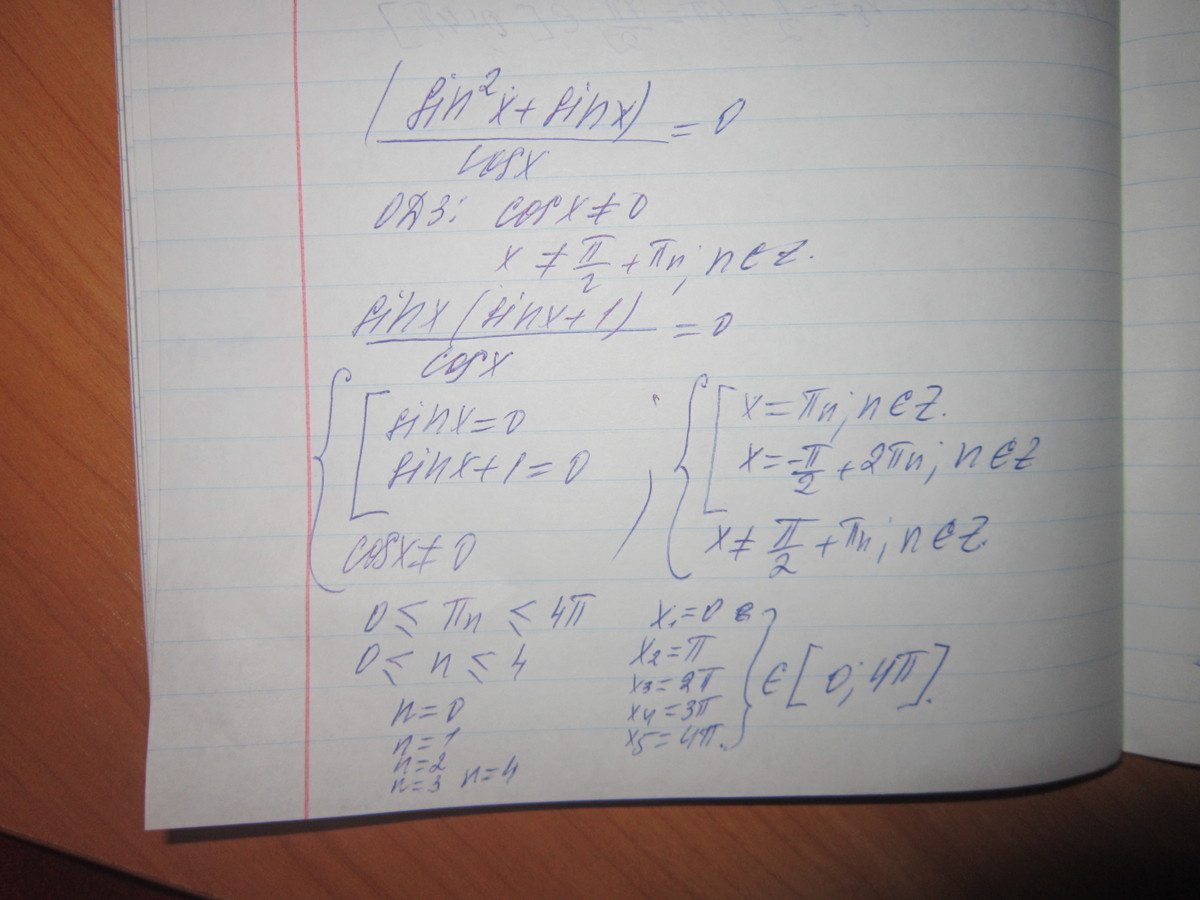

Автор ответа:
0
Уравнение (sin^2 x + sinx) cosx =0 можно преобразовать:
sin x(sin x+1) cos x =0
(sin x/ cos x)*(sin x+1) =0
tg x*(sinx+1) = 0
Отсюда следуют два решения:
х = arc tg 0 = 0; 1пи; 2пи; 3пи; 4пи
x = arc sin (-1) = 3/2пи; 7/2пи
Итого - 7 корней.
sin x(sin x+1) cos x =0
(sin x/ cos x)*(sin x+1) =0
tg x*(sinx+1) = 0
Отсюда следуют два решения:
х = arc tg 0 = 0; 1пи; 2пи; 3пи; 4пи
x = arc sin (-1) = 3/2пи; 7/2пи
Итого - 7 корней.
Приложения:
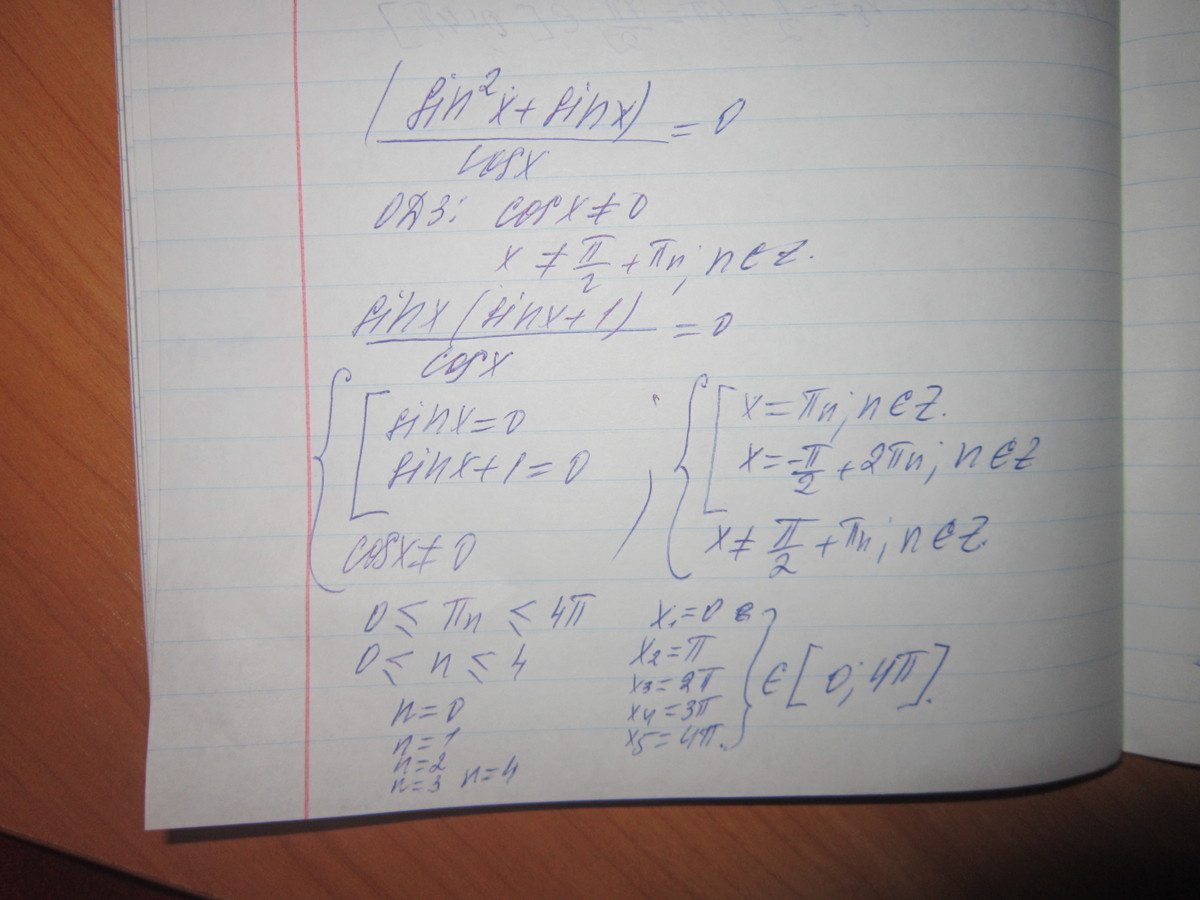

Похожие вопросы
Предмет: Русский язык,
автор: us261003
Предмет: Английский язык,
автор: Аноним
Предмет: Геометрия,
автор: vikkab74Vikila
Предмет: Обществознание,
автор: 12329
Предмет: Обществознание,
автор: fusya97