Предмет: Геометрия,
автор: mashkovamarina
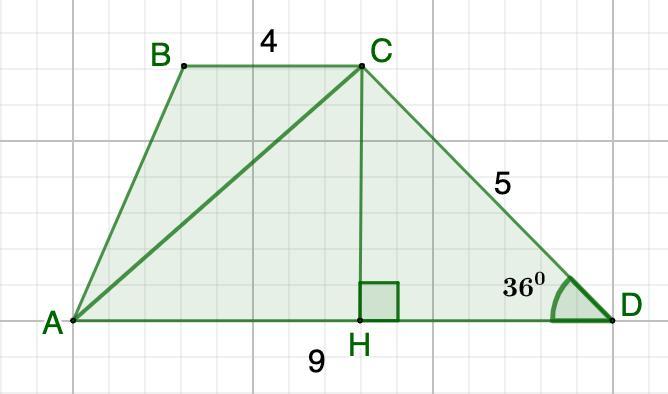
Найдите площадь и меньшую диагональ трапеции ,если ее основания 4см и 9см, большая боковая сторона 5см, а прилежащий к ней угол 36°
Ответы
Автор ответа:
5
Ответ:
АС≈5,75 cм
S=19,18 см²
Объяснение:
Дано: ABCD - трапеция.
ВС=4 см; АD=9 см; СD=5 см.
∠D=36°
Найти: АС, .
Решение:
sin36°≈0,59
cos36°≈0,81
1. Рассмотрим ΔАСD.
Найдем АС по теореме косинусов:
АС²=АD²+СD²-2·АD·СD·cos36°=81+25-2·9·5·0,81≈33,1
⇒ АС≈5,75 (cм)
2. Проведем высоту СН.
Рассмотрим ΔНСD:
Синус угла - отношение противоположного катета к гипотенузе.
(см)
3. Найдем площадь трапеции.
Площадь трапеции равна произведению полусуммы оснований на высоту.
(см²)
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: алекс84
Предмет: Химия,
автор: kakumza00
Предмет: Геометрия,
автор: Ваня2142
Предмет: Английский язык,
автор: kirilldanilov1
Предмет: Алгебра,
автор: fifthdoctor