Предмет: Алгебра,
автор: Stre1la
Сделайте пожалуйста 3
Приложения:
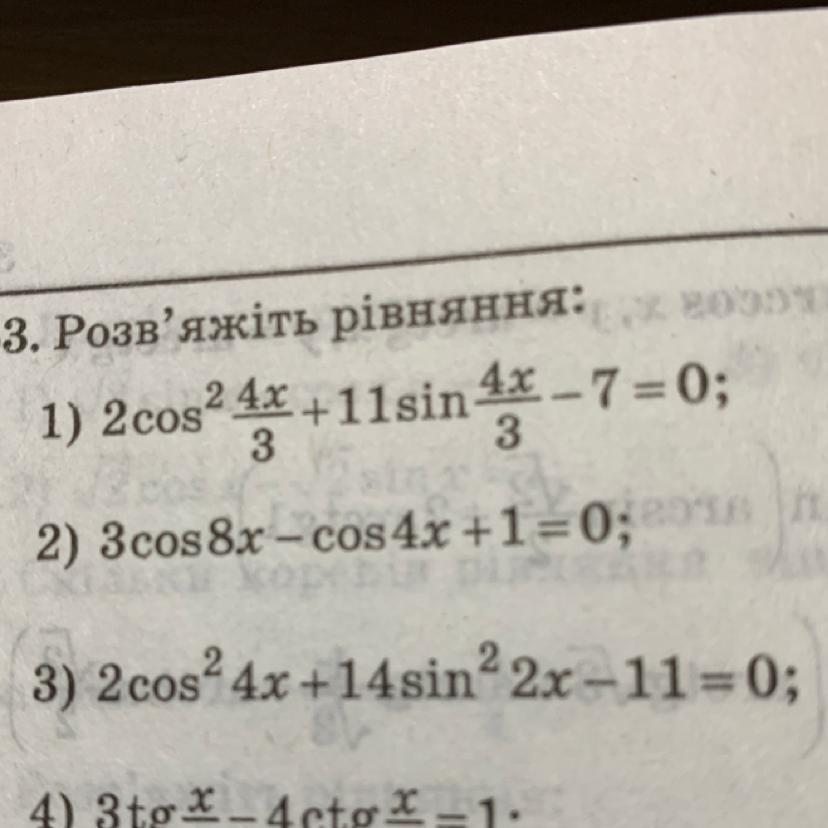
Miroslava227:
третье уравнение или все три уравнения?
Только 3
Ответы
Автор ответа:
0
Ответ:
n принадлежит Z.
Похожие вопросы
Предмет: Русский язык,
автор: Мария06312
Предмет: Английский язык,
автор: PolinkaPolinka23
Предмет: Алгебра,
автор: Zhenja98
Предмет: Математика,
автор: КаринаКозлова
Предмет: Математика,
автор: Kanztavar