Предмет: Математика,
автор: helpmeplease44343
Найти для функции y'x и y''x
Приложения:
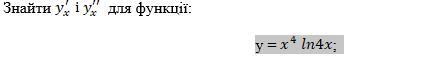
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Химия,
автор: juliaobukhjva2
Предмет: Химия,
автор: Лицеистка7
Предмет: Физика,
автор: Gluoxy
Предмет: Биология,
автор: Пикселькина
Предмет: Українська мова,
автор: nikov2791