Предмет: Математика,
автор: AYAAYRA
Решите данное неравенство
Приложения:
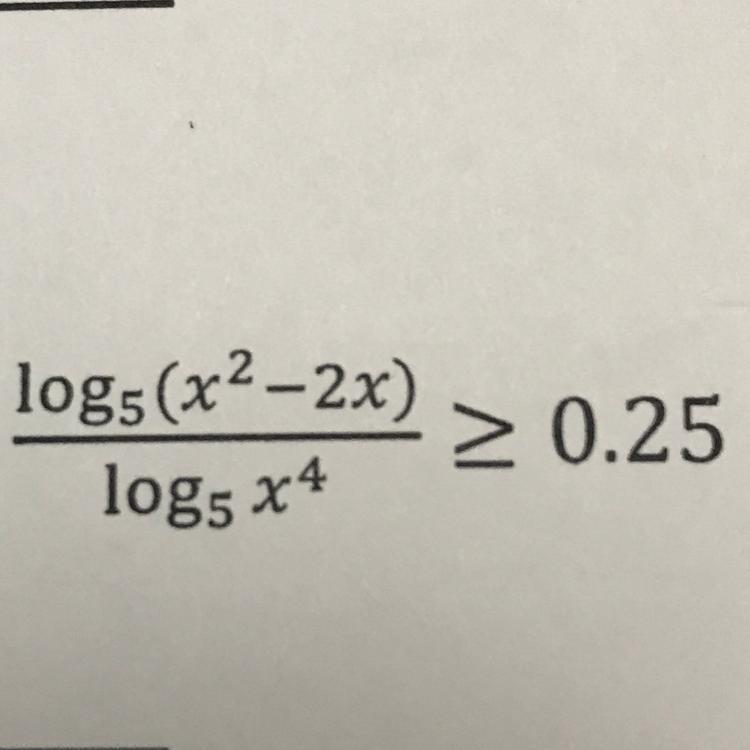
Ответы
Автор ответа:
4
Область допустимых значений дроби:
Область допустимых значений логарифмических выражений:
ОДЗ:
=================================
Воспользуемся формулой:
=================================
Заменим логарифмическое неравенство равносильным с учетом ОДЗ (метод рационализации):
Третья скобка всегда положительна, на общий знак выражения не влияет, можно опустить.
1) Раскрываем модуль для положительных значений x:
С учетом ОДЗ:
2) Раскрываем модуль для отрицательных значений x:
С учетом ОДЗ:
Ответ:
olgaua64:
Разве -1/2 не подходит? Ответ не полний!!!
Подставьте и посчитайте, дробь будет отрицательной. Отрицательное число не может быть больше положительного. Число -1/2 не подходит.
здравствуйте,зайдите пж в директ
хERISx здравствуйте,можете мне помочь пж с новым вопросом
Похожие вопросы
Предмет: Математика,
автор: fvbyrf005
Предмет: Алгебра,
автор: vadymok
Предмет: Математика,
автор: igorx2004
Предмет: Физика,
автор: dimooon4
Предмет: Обществознание,
автор: ВикаМаурер2005