Предмет: Алгебра,
автор: dubrovskiidanil
Решите плиз
Буду благодаре
Очень
Приложения:

Ответы
Автор ответа:
0
1)Корень 4 степени из (3a^2b^3) * корень 4 степени из (27a^2b) = корень 4 степени из (81a^4b^4) = 3|a||b|
Здесь я воспользовался тем, что произведение корней равно корню произведения, а также, что корень 4 степени из 4 степени выражения равен модулю этого выражения.
2)log(12) 2 + log(12)72 = log(12) (72 * 2) = log(12) 144 = 2
Здесь я воспользовался одним из свойств логарифма, а именно, что логарифм произведения равен сумме логарифмов, только в обратном порядке.
3)Возведём обе части этого уравнения в квадрат:
x + 4 = 64
x = 60
Сделаем проверку:
корень из (60 + 4) = 8
корень из 64 = 8 - верно
Ответ:8
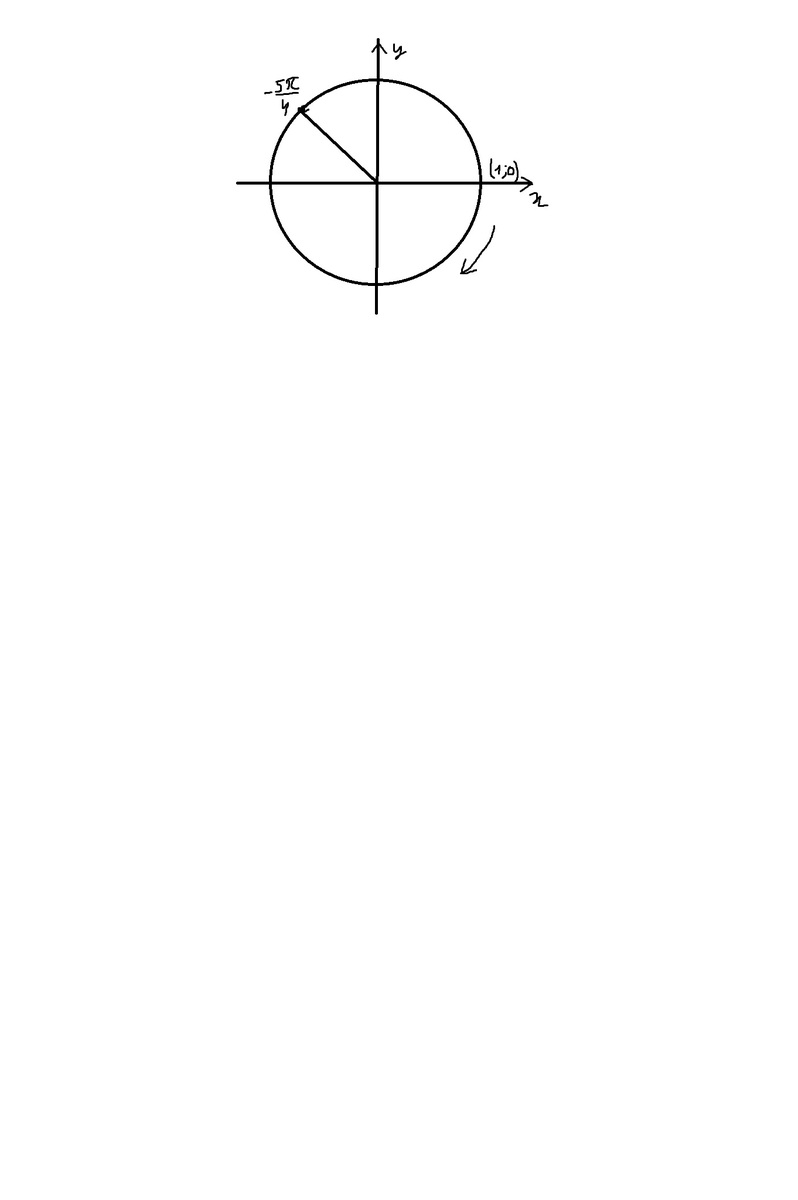
5)Решение пятого задания - построенная точка.
6)Сначала найдём ОДЗ данного уравнения. Так как у нас стоит выражение под знаком логарифма, то я просто обязан потребовать, чтобы 3x-1>0, отсюда x > 1/3
теперь решаем уравнение:
3x-1 = 10^0
3x - 1 = 1
3x = 2
x = 2/3 - наш корень удовлетворяет ОДЗ.
Ответ:2/3
7)Пусть 4^x = t, t > 0
Тогда выходим на обыкновенное квадратное уравнение относительно t, которое и решаем:
t^2 - 17t + 16 = 0
t1 = 16; t2 = 1
Возвращаясь теперь к переменной x, получаю:
4^x = 16 или 4^x = 1
x = 2 x = 0
Ответ: 0;2
Здесь я воспользовался тем, что произведение корней равно корню произведения, а также, что корень 4 степени из 4 степени выражения равен модулю этого выражения.
2)log(12) 2 + log(12)72 = log(12) (72 * 2) = log(12) 144 = 2
Здесь я воспользовался одним из свойств логарифма, а именно, что логарифм произведения равен сумме логарифмов, только в обратном порядке.
3)Возведём обе части этого уравнения в квадрат:
x + 4 = 64
x = 60
Сделаем проверку:
корень из (60 + 4) = 8
корень из 64 = 8 - верно
Ответ:8
5)Решение пятого задания - построенная точка.
6)Сначала найдём ОДЗ данного уравнения. Так как у нас стоит выражение под знаком логарифма, то я просто обязан потребовать, чтобы 3x-1>0, отсюда x > 1/3
теперь решаем уравнение:
3x-1 = 10^0
3x - 1 = 1
3x = 2
x = 2/3 - наш корень удовлетворяет ОДЗ.
Ответ:2/3
7)Пусть 4^x = t, t > 0
Тогда выходим на обыкновенное квадратное уравнение относительно t, которое и решаем:
t^2 - 17t + 16 = 0
t1 = 16; t2 = 1
Возвращаясь теперь к переменной x, получаю:
4^x = 16 или 4^x = 1
x = 2 x = 0
Ответ: 0;2
Приложения:
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Физика,
автор: aurumtv1221
Предмет: Английский язык,
автор: 10010101020oria17
Предмет: Химия,
автор: Арсеноя
Предмет: История,
автор: Кисямурлыся