Предмет: Математика,
автор: motorny0919
Найти общее (частичный) решение уравнения.
Приложения:
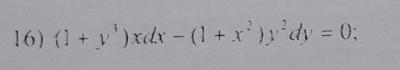
Ответы
Автор ответа:
2
Ответ:
общее решение
Похожие вопросы
Предмет: Геометрия,
автор: ronaldweasley2
Предмет: Математика,
автор: Андрей1001100101
Предмет: Математика,
автор: LSDPrizrakRem1x
Предмет: Математика,
автор: MelkayN
Предмет: Алгебра,
автор: mscity05