Предмет: Геометрия,
автор: Darkep
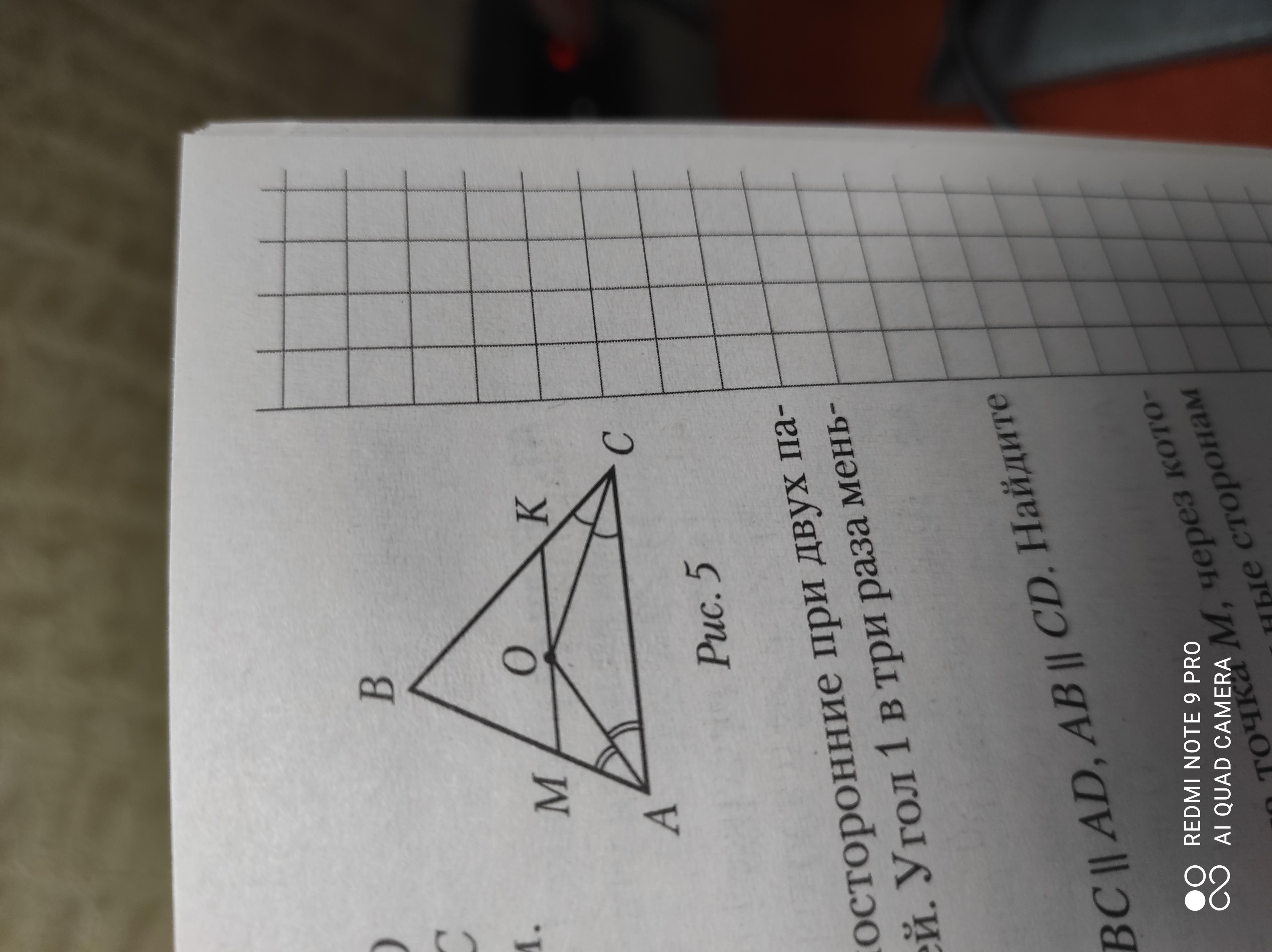
На рисунке 5 MK || AC, AO и CO - биссектрисы углов BAC и BCA, AM= 3 см, KC=5см. Найдите MK.
1)3
2)4
3)5
4)8
Все в см
Приложения:
Ответы
Автор ответа:
5
Ответ:
MK = 8 см
Объяснение:
Дано: MK || AC, AM = 3 см, KC = 5 см, ∠MAO = ∠CAO, ∠ACO = ∠KCO
Найти: MK - ?
Решение: Так как по условию MK || AC, то ∠CAO = ∠MOA, ∠ACO = ∠KOC как внутренние разносторонние углы при секущей. Рассмотрим треугольники ΔMOA и ΔKOC. Так как ∠CAO = ∠MOA, ∠ACO = ∠KOC, то согласно теореме треугольники являются равнобедренными с основаниями AO и OC соответственно, тогда у равнобедренных треугольников соответствующие стороны равны и MA = MO, KO = KC.
MK = MO + OK = MA + KC = 5 + 3 = 8 см.
Похожие вопросы
Предмет: Математика,
автор: valerochkaavra
Предмет: Литература,
автор: a20n
Предмет: Английский язык,
автор: LuGlSer
Предмет: Математика,
автор: екатерина220613
Предмет: Музыка,
автор: Natalia14505