!ОЧЕНЬ СРОЧНО! 35 БАЛЛОВ!
Решите уравнение, используя способ замены переменной. с подробным решением.
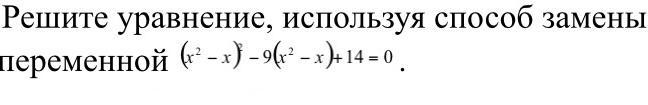
Ответы
Метод замены переменной используется в том случае, когда уравнение можно привести к виду квадратного. В условии задачи есть подсказка, указывающая на одинаковые многочлены вознесённые во вторую и первую степень, их то мы и можем заменить на любую произвольную переменную (обычно используют t)
Тогда, пусть х²-х = t , получаем :
(t)² -9*(t) +14 = 0 (скобки в данном случае не обязательно писать, но для наглядности всё же можно)
решим уравнение относительно t:
t² - 9t + 14 = 0
D = 81 - 4*14 = 81-56 = 25
√D = 5
t1 = (9+5)/2 = 7
t2 = (9-5)/2 = 2
Если мы делаем замену переменную мы ВСЕГДА должны вернуться к изначальной переменной [ведь нам в ответе нужно указать чему равен х, а не t :) ]
x²-x = 7
x²-x = 2
Нужно решить оба уравнения, и все корни которые мы получим будут являться решением исходного уравнения.
1) х²-х -7 = 0
D = 1 -4*(-7) = 29
√D = √29
x1 = (1+√29)/2
x2 = (1-√29)/2
2) x²-x-2=0
D = 1 -4*(-2) = 9
√D=3
x3 = (1+3)/2 = 2
x4 = (1-3)/2 = -1
В ответ указываем все четыре корня. Данное уравнение сложно решить иным способом. Если начать раскрывать скобки получится очень "некрасивый" многочлен четвертой степени