Предмет: Математика,
автор: maxambrosii
Исследовать на экстремум функцию:
Приложения:
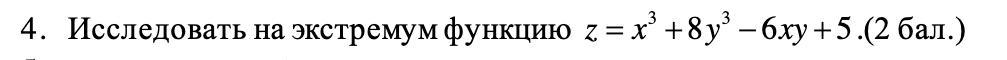
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
ищем kритические точки
решаем систему
имеем две критические точки М₁ (0;0) и М₂(1;0,5)
теперь определимся, где минимум, где максимум
AC - B² = -36 < 0 глобального экстремума нет.
AC - B²= 108 > 0 и A > 0 , в точке M₂(1;0.5) имеется минимум
z(1;0.5) = 4
Похожие вопросы
Предмет: Геометрия,
автор: julia0205
Предмет: Алгебра,
автор: Аноним
Предмет: Математика,
автор: terilis15
Предмет: Математика,
автор: karinaovodkovap3bh50