Предмет: Геометрия,
автор: dada561
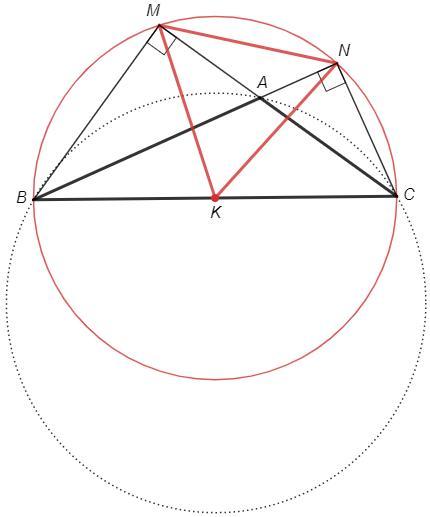
В треугольнике АВС угол А равен 120. ВM и CN высоты треугольника. Точка К
середина стороны ВС
a ) Докажите что треугольник KMN - равносторонний
б) Найдите площадь треугольника KMN, если радиус окружности. описанной вокруг треугольника ABC, равен 2корень(3).
Ответы
Автор ответа:
3
а)
Отрезок BC виден из точек M и N под прямым углом - точки M и N лежат на окружности с диаметром BC.
Точка K - середина диаметра - центр окружности.
Найдем ∠BAC как угол между хордами BN и CM
∠BAC =(∪BC+∪MN)/2 => ∪MN =2∠BAC -∪BC =120*2 -180 =60°
KM=KN (радиусы), ∠MKN=∪MN=60 (центральный угол) =>
△KMN - равнобедренный с углом 60 - равносторонний.
б)
Теорема синусов
BC/sin(BAC) =2R => BC =2 *2√3 *√3/2 =6
KM =BC/2 =3
Площадь равностороннего треугольника
S(KMN) =√3/4 KM^2 =9√3/4
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: lubasergeeva73
Предмет: Литература,
автор: bww2401
Предмет: Математика,
автор: Эвелиночка11
Предмет: Математика,
автор: Maripolaretasa