Предмет: Математика,
автор: karina200320000
ПОЖАЛУЙСТА МАТЕМАТИКУ РЕШИТЕ ДАЮ 20 БАЛЛОВ
Приложения:
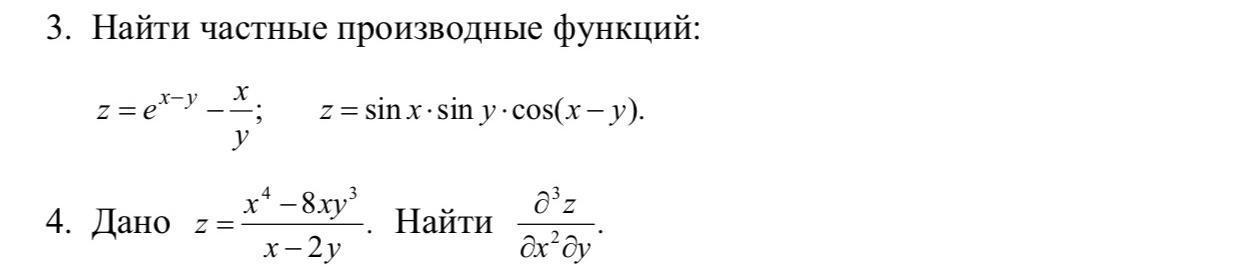
Ответы
Автор ответа:
1
Ответ:
3)
1.
2.
4)
karina200320000:
Спасибо
Похожие вопросы
Предмет: Химия,
автор: Kirashima
Предмет: Химия,
автор: joker095
Предмет: Другие предметы,
автор: lanamchedlidze
Предмет: История,
автор: egor741852963
Предмет: Информатика,
автор: maksim26112007