Предмет: Алгебра,
автор: Mixtit
Найти общее решение (общий интеграл) для дифференциального уравнения,
допускающего понижение порядка.
Приложения:
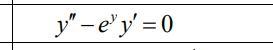
Ответы
Автор ответа:
0
Ответ:
понижаем порядок:
Mixtit:
Огромное спасибо
Я тебя люблю
Похожие вопросы
Предмет: Математика,
автор: СупЕрУм5
Предмет: Русский язык,
автор: nurainasaulebai2001
Предмет: Математика,
автор: adilyanasybuli
Предмет: Математика,
автор: яя82
Предмет: Физика,
автор: anyanela2004