Предмет: Алгебра,
автор: sashaostrynska12
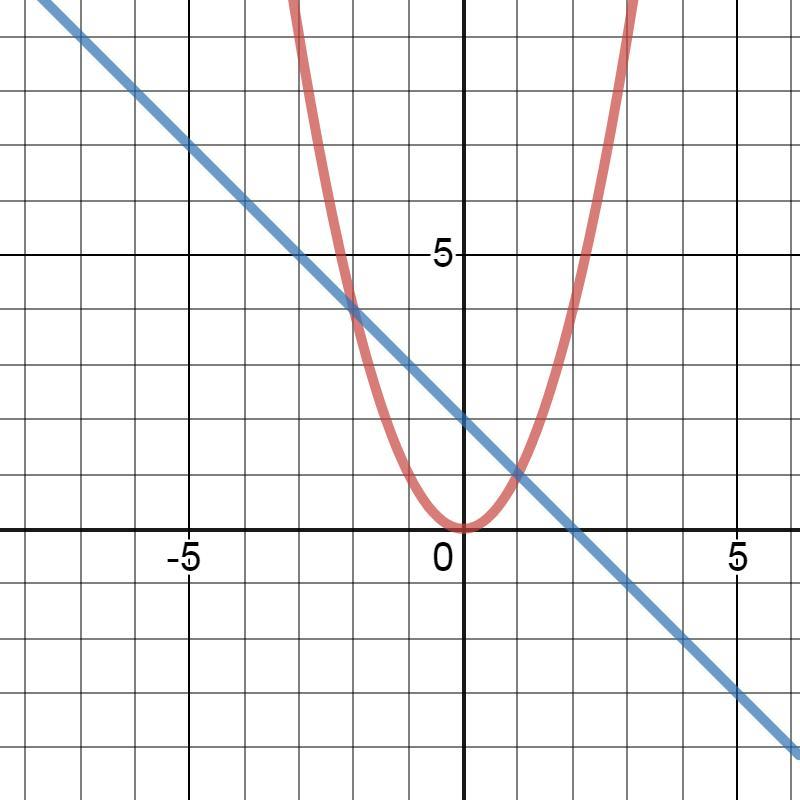
знайти площу фігури обмеженої лініями:
y=x2; y=2-x;
Ответы
Автор ответа:
1
Объяснение:
Ответ: S=4,5 кв. ед.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: nathal97071
Предмет: История,
автор: nik0602
Предмет: Русский язык,
автор: MILENA2221
Предмет: Химия,
автор: Mubareka
Предмет: Математика,
автор: Ulya2484