Предмет: Математика,
автор: tvkitay
100б, Найти второй дифференциал функции
Приложения:
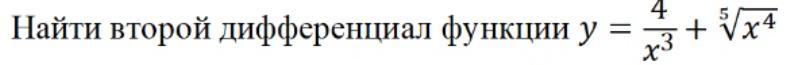
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: История,
автор: Хомяк26
Предмет: Математика,
автор: drm74
Предмет: География,
автор: amirova200250
Предмет: Математика,
автор: МамедовНурлан
Предмет: Алгебра,
автор: nice61