Предмет: Алгебра,
автор: azat1495
2.136. Найдите корни уравнения (1,2)
Приложения:
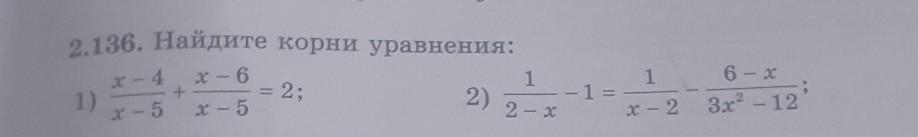
Ответы
Автор ответа:
7
1)
2)
azat1495:
спасибо
можешь 3,4,5
Похожие вопросы
Предмет: Русский язык,
автор: kremarenka
Предмет: Химия,
автор: tairivakamila
Предмет: Английский язык,
автор: Conia569
Предмет: Математика,
автор: Аноним