Предмет: Алгебра,
автор: kirill4558
Найти пределы ( не пользуясь правилом Лопиталя)
На фото(20 вариант 4,5 пункт решить надо) очень срочно
Приложения:
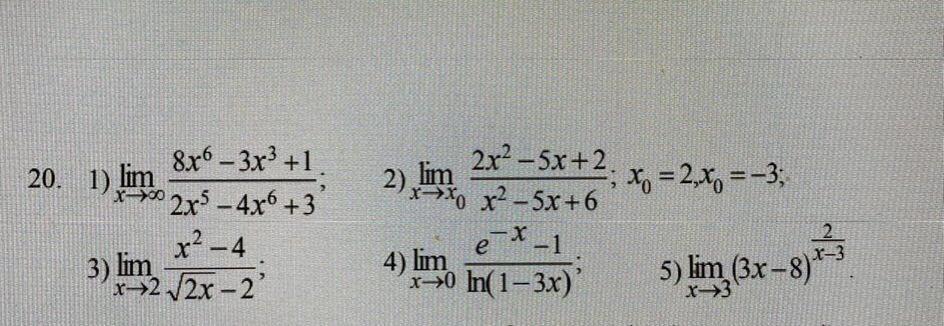
Ответы
Автор ответа:
1
Ответ:
При решении 1 примера пользуемся правилом замены бесконечно малых величин на эквивалентные бесконечно малые . А при решении 2 примера пользуемся вторым замечательным пределом .
Похожие вопросы
Предмет: Информатика,
автор: ElizabetFox
Предмет: Математика,
автор: aidana2003ah
Предмет: Алгебра,
автор: Аноним
Предмет: Математика,
автор: Victorpak2005
Предмет: Математика,
автор: azzero68