Предмет: Математика,
автор: Czaryok
ПОМОГИТЕ! Найти сумму ряда.
Приложения:
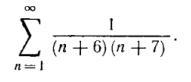
Czaryok:
Доказать сходимость ряда и найти его сумму
Ответы
Автор ответа:
2
Ответ:
Пошаговое объяснение:
А значит
Огромное спасибо
Похожие вопросы
Предмет: Русский язык,
автор: litvalieva
Предмет: Математика,
автор: Аноним
Предмет: Английский язык,
автор: arkatova011
Предмет: Литература,
автор: ольга1651