Предмет: Алгебра,
автор: happyms
Найти производные dy/dx с объяснением (шагами):
Приложения:
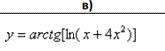
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: idriganets
Предмет: Русский язык,
автор: ctacyan
Предмет: Физика,
автор: Nebydos
Предмет: Математика,
автор: Пончик3210
Предмет: Математика,
автор: sofiaznanijacom