помогите срочно даю 40 баллов
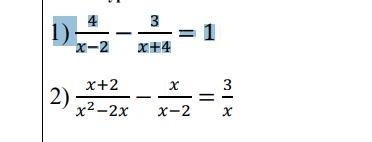
Ответы
Ответ:
В решении.
Объяснение:
Решить уравнение:
1) 4/(х - 2) - 3/(х + 4) = 1
Умножить уравнение (все части) на (х - 2)(х + 4), чтобы избавиться от дробного выражения:
4 *(х + 4) - 3 *(х - 2) = 1 * (х - 2)(х + 4)
Раскрыть скобки:
4х + 16 - 3х + 6 = х² + 4х - 2х - 8
Привести подобные члены:
х + 22 = х² + 2х - 8
-х² + х - 2х + 22 + 8 = 0
-х² - х + 30 = 0/-1
х² + х - 30 = 0, квадратное уравнение, ищем корни:
D=b²-4ac = 1 + 120 = 121 √D= 11
х₁=(-b-√D)/2a
х₁=(-1-11)/2
х₁= -12/2
х₁= -6;
х₂=(-b+√D)/2a
х₂=(-1+11)/2
х₂=10/2
х₂=5.
Проверка путём подстановки вычисленных значений х в уравнение показала, что данные решения удовлетворяют данному уравнению.
2) (х + 2)/(х² - 2х) - х/(х - 2) = 3/х
(х + 2)/х(х - 2) - х/(х - 2) = 3/х
Умножить уравнение (все части) на х(х - 2), чтобы избавиться от дробного выражения:
(х + 2) - х * х = 3 * (х - 2)
Раскрыть скобки:
х + 2 - х² = 3х - 6
Привести подобные члены:
-х² + х - 3х + 2 + 6 = 0
-х² - 2х + 8 = 0/-1
х² + 2х - 8 = 0, квадратное уравнение, ищем корни:
D=b²-4ac = 4 + 32 = 36 √D= 6
х₁=(-b-√D)/2a
х₁=(-2-6)/2
х₁= -8/2
х₁= -4;
х₂=(-b+√D)/2a
х₂=(-2+6)/2
х₂=4/2
х₂=2.
По ОДЗ х не может быть равен 2, так как дробь в этом случае не имеет смысла, поэтому решение уравнения х= -4.
Проверка путём подстановки вычисленного значения х в уравнение показала, что данное решение удовлетворяет данному уравнению.