Question

Помогите решить задачу.
В равнобедренной трапеции ABCD : AB параллельно CD, AB=AC и AD=DC. Найдите угол при меньшем основании трапеции.  

Answer 1

 В трапеции АВСD два равнобедренных по условию треугольника : САВ и СDA 
В равнобедренном треугольнике СDА
∠DСА= ∠DАС, но они равны также углу САВ треугольника САВ,  
так как.
∠DСА и ∠САВ - накрестлежащие углы при параллельных  основаниях и секущей -диагонали АС. ( отсюда АС - биссектриса угла DАВ)
∠DАВ= ∠СВА по свойству углов равнобедренной трапеции. 
∠САВ=0,5∠ DАВ= 0,5∠СВА
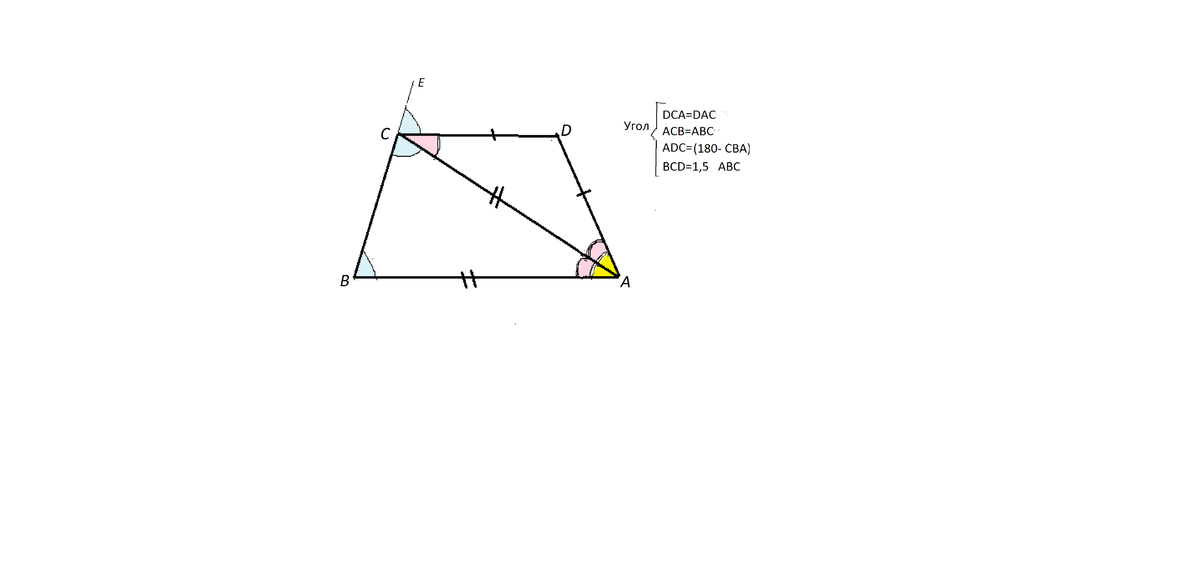
Продолжим ВС до Е. 
∠ЕСD= ∠СВА ( ВЕ - секущая при СD и АВ). 
∠СВА = ∠ВСА - углы равнобедренного треугольника АВС
Развернутый ∠ЕСВ=180 =2 ∠АВС +0,5∠АВС 
∠ ЕСВ=2,5 ∠ АВС
∠DСВ=∠АDС= ∠СВА+∠DСА= ∠СВА+0,5 ∠АВС=1,5 ∠АВС

∠ВСА= ∠ЕСВ:2,5= 72°.  
∠BСD=∠АDС=72*1,5=108°