Question

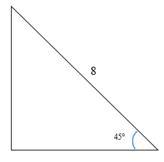
Найдите площадь треугольника по данным рисунка.

Answer 1

Дано:

Прямоугольный треугольник АВС

угол С = 90 градусов,

АВ — гипотенуза,

АВ = 8,

угол А = 45 градусов.

Найти площадь треугольника АВС, то есть S АВС — ?

Решение:

1. Рассмотрим прямоугольный треугольник АВС. Сумма градусных мер углов треугольника равна 180 градусов. Тогда угол В = 180 - угол А - угол С;

угол В = 180 - 45 - 90;

угол В = 45 градусов.

Следовательно прямоугольный треугольник АВС является еще и равнобедренным, тогда АС = ВС.

2. По теореме Пифагора (квадрат гипотенузы равен сумме квадратов катетов):

АС^2 + ВС^2 = АВ^2 ( пусть АВ = ВС = х сантиметров);

х^2 + х^2 = 8^2 ;

2 * х^2 = 64;

х^2 = 64 : 2;

х^2 = 32.

3. S АВС = 1/2 * АС * ВС;

S АВС = 1/2 * 32;

S АВС = 16.

Ответ: 16.

Answer 2

Ответ:

16ед²

Объяснение:

Треугольник равнобедренный, прямоугольный.

Пусть катет будет х, тогда второй катет тоже х, так как треугольник равнобедренный.

По теореме Пифагора составляем уравнение.

х²+х²=8²

2х²=64

х²=64/2

х=√32

х=4√2 ед катет равнобедренного треугольника

Площадь прямоугольного треугольника равна половине произведения двух катетов.

S=1/2*(4√2)²=16*2/2=16 ед²