Предмет: Математика,
автор: kobylchenkovika
Помогите пожалуйста.... Найти производные dy/dx следующих функций
Приложения:
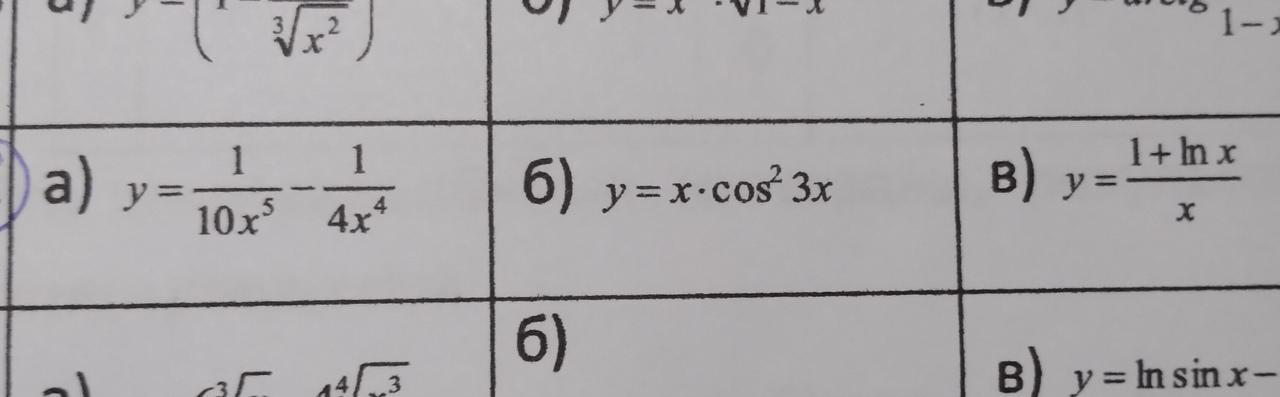
Ответы
Автор ответа:
1
Ответ:
а)
б)
в)
Похожие вопросы
Предмет: Физика,
автор: NastyaDenisova836
Предмет: Українська література,
автор: kurilovich20044
Предмет: Математика,
автор: KristinaCats
Предмет: Химия,
автор: mabelprincess