Предмет: Геометрия,
автор: ivleekaterina
Дано треугольник abc d принадлежит ab e принадлежит ac, bc принадлежит альфа, альфа параллельна de, de = 5 см bd/da=2/3 найти bc
Ответы
Автор ответа:
1
Ответ:
ед.
Объяснение:
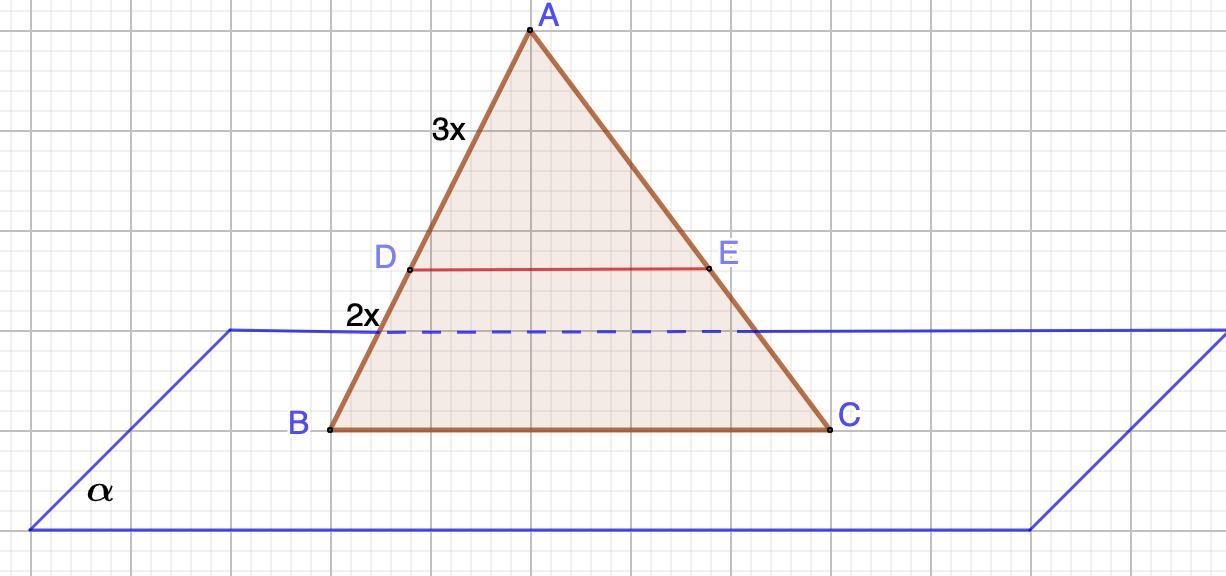
Дано: ΔАВС.
DE ∈ α; DE = 5;
BD : DA = 2 : 3
Найти: ВС
Решение:
- Прямая параллельна плоскости, если она параллельна какой-нибудь прямой, лежащей в этой плоскости.
⇒ DE || BC;
- Лемма. Если две стороны треугольника пересекает прямая, параллельная третьей стороне, то она отсекает треугольник, подобный данному.
⇒ ΔDAE ~ ΔBAC
Пусть BD = 2x, тогда DA = 3x ⇒ AB = 5x
Составим отношение сходственнах сторон:
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: kate20151
Предмет: Математика,
автор: Олеся11205
Предмет: Русский язык,
автор: olya6776
Предмет: Литература,
автор: 510011Егор