Предмет: Математика,
автор: mishadr2
Помогите решить дифференциальное уравнение с разделяющимися переменными
Приложения:
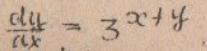
Ответы
Автор ответа:
0
Ответ:
общее решение
Похожие вопросы
Предмет: Русский язык,
автор: vikulka96
Предмет: Биология,
автор: chimyrbaeva023
Предмет: Математика,
автор: katyahamster
Предмет: Геометрия,
автор: alla096
Предмет: Математика,
автор: arutoganisan25