Предмет: Геометрия,
автор: nejmn761
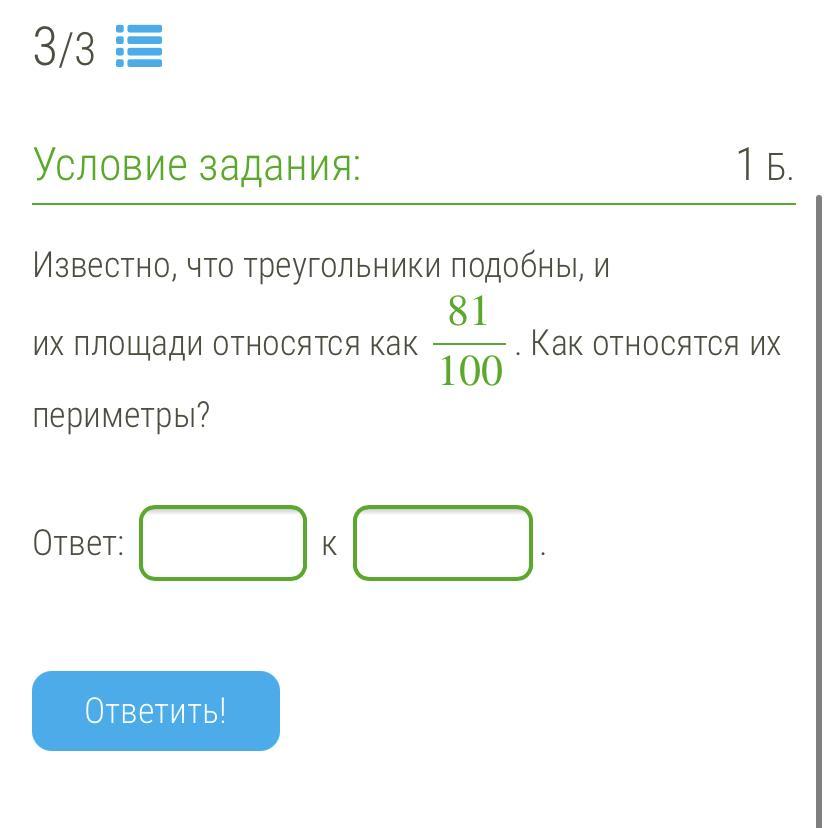
Известно, что треугольники подобны, и их площади относятся как 81100. Как относятся их периметры?
ЛАЛАОАООАОАО ПОМОГИТЕ
Приложения:
Ответы
Автор ответа:
1
Ответ:
Объяснение:
- Площади подобных треугольников относятся друг к другу в отношении, равном квадрату коэффициента подобия:
- Отношение периметров двух подобных треугольников равно коэффициенту подобия треугольников
Похожие вопросы
Предмет: Математика,
автор: Valent787
Предмет: Математика,
автор: Asus001
Предмет: Алгебра,
автор: Аноним
Предмет: Математика,
автор: Chigetta