Предмет: Математика,
автор: kirillpopov673
Помогите пожалуйста, вычислить площадь фигуры, ограниченной параболами и построить чертеж.
Приложения:
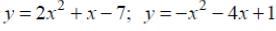
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
y₁ = -x²-4x+1 ; y₂=2x² +x-7
находим точки пересечения
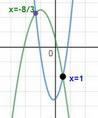
2x² +x-7 = -x²-4x+1 ⇒ 3x² +5x-8=0 ⇒ x₁ = -8/3; x₂=1
теперь найдем у₁ - у₂ = -x²-4x+1 -(2x² +x-7 ) = -3x² -5x+8
и теперь площадь фигуры
Приложения:
kirillpopov673:
А что за фигура ограничена параболами ?
да не знаю я как она называется. вот этот похожий на эллипс...
А все понял
ок -)))
Похожие вопросы
Предмет: Математика,
автор: islammilana20
Предмет: Українська мова,
автор: Karinaisclever
Предмет: Математика,
автор: Танюша546
Предмет: Математика,
автор: Никогр
Предмет: История,
автор: Аноним