Question

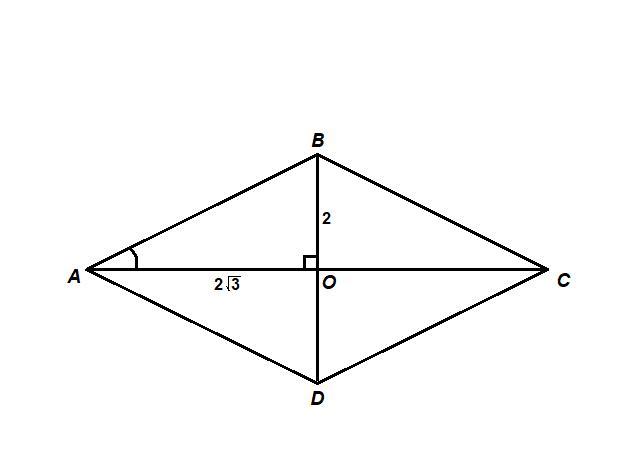
5.Найдите углы ромба ABCD, если его диагонали AC и BD равным 4√3 и 4

Answer 1

Ответ:

∠BCD = ∠BAD = 60°

∠ADC = ∠ABC = 120°

Объяснение:

Диагонали ромба взаимно перпендикулярны и делятся точкой пересечения пополам.

АО = 0,5 · АС = 0,5 · 4√3 = 2√3

ВО = 0,5 · BD = 0,5 · 4 = 2

ΔАОВ:  ∠АОВ = 90°,

  $tg\angle OAB=\dfrac{OB}{OA}=\dfrac{2}{2\sqrt{3}}=\dfrac{1}{\sqrt{3}}$

∠OAB = 30°

Диагонали ромба лежат на биссектрисах его углов, поэтому

∠BAD = 2 · ∠OAB = 2 · 30° = 60°

Сумма углов, прилежащих к одной стороне ромба, равна 180°.

∠АВС = 180° - ∠BAD = 180° - 60° = 120°

Противолежащие углы ромба равны:

∠BCD = ∠BAD = 60°

∠ADC = ∠ABC = 120°