Question

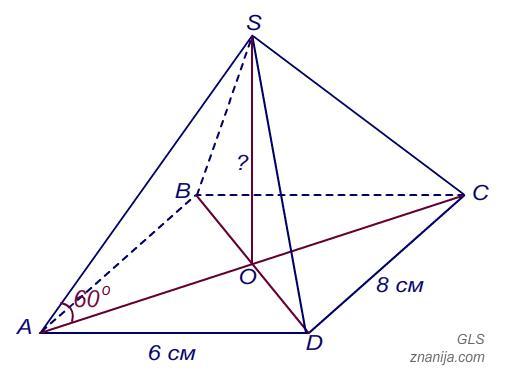
Основою піраміди є прямокутник зі сторонами 6 см і 8 см а кожне бічне ребро утворюе з площиною основи кут 60 . Знайдіть висоту піраміди.

Answer 1

Ответ:

Высота пирамиды равна $\displaystyle 5\sqrt{3}$ см.

Объяснение:

Дано: пирамида SABCD; ABCD - прямоугольник, основание пирамиды; стороны основания AD = 6 см, DC =  8 см; каждое боковое ребро образует с плоскостью основания угол 60°.

Найти: высоту пирамиды.

Решение.

По условию каждое боковое ребро образует с плоскостью основания угол 60° ⇒

В ΔASC  ∠SAC = ∠SCA = 60°, ΔASC равнобедренный, а отрезок SO, проходящий через середину AC (точку O) является медианой, биссектрисой, высотой.

В ΔBSD  ∠SBD = ∠SDB = 60°, ΔBSD равнобедренный, а отрезок SO, проходящий через середину BD (точку O) является медианой, биссектрисой, высотой.

• Признак перпендикулярности прямой и плоскости: если прямая перпендикулярна к двум пересекающимся прямым, лежащим в одной плоскости, то она перпендикулярна к этой плоскости.

⇒ SO ⊥ плоскости основания прямоугольника ABCD, и является высотой пирамиды.

AC и BD диагонали основания - прямоугольника ABCD, пересекаются в точке O, которая является проекцией точки S на плоскость основания пирамиды.

Из прямоугольного ΔADC по т.Пифагора найдем гипотенузу AC (диагональ основания):

AC² = AD² + DC² = 36 + 64 = 100;

AC = 10 см.

В ΔSAO  ∠SOA = 90°, ∠SAO = 60°,

AO = AC : 2 = 10 см : 2 = 5 см.

$\displaystyle tg(\angle SAO) = \frac{SO}{AO} ;\\\\ tg(60^{o}) = \frac{SO}{5}=\sqrt{3} ;\\\\SO=5\sqrt{3} \;(cm).$

Высота пирамиды равна $\displaystyle 5\sqrt{3}$ см.