Предмет: Математика,
автор: Аноним
Найти общее решение ДР и частное решение, которое проходит через точку М (2, 4)
Приложения:
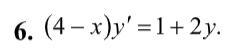
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: надддя
Предмет: Русский язык,
автор: maismamedov01
Предмет: Алгебра,
автор: AnastaSiaorta2
Предмет: Биология,
автор: anelechka0110