Предмет: Алгебра,
автор: dashacot66
Помогите пожалуйста!!! Алгебра
Приложения:
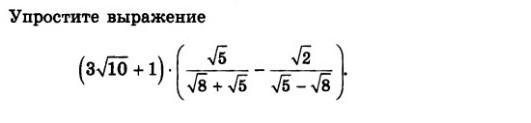
Ответы
Автор ответа:
1
dashacot66:
спасибо огромное!!!!
Похожие вопросы
Предмет: Математика,
автор: vasilievaolga3
Предмет: Математика,
автор: vasilievaolga3
Предмет: Русский язык,
автор: vefahesenova
Предмет: Математика,
автор: coolendermanYT