Предмет: Геометрия,
автор: oran9ejuice
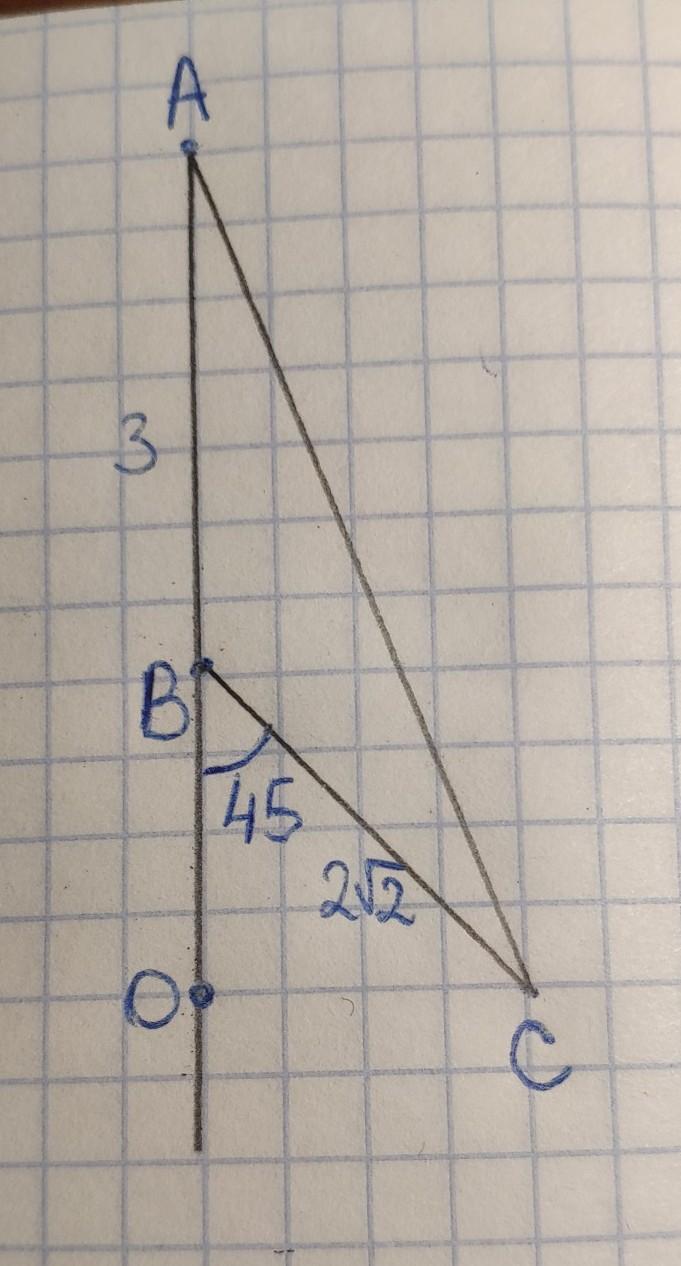
В треугольнике АВС АВ = 3 см, ВС =2 2 .Внешний угол при вершине В равен 45°. Найдите длину АС.
2 .Внешний угол при вершине В равен 45°. Найдите длину АС.
Ответы
Автор ответа:
5
Ответ:
Угол ОВС+угол АВС=180°, так как это смежные углы. Следовательно угол АВС=180°–угол ОВС=180°–45°=135°
По теореме косинусов в ∆АВС:
Совокупность:
АС=√29
АС=–√29
Так как длина задана положительным числом, то АС=√29.
Ответ: √29
Приложения:
Аноним:
спасибо
Похожие вопросы
Предмет: География,
автор: irinam2002
Предмет: Экономика,
автор: 3112оля
Предмет: Математика,
автор: Аноним
Предмет: Биология,
автор: шаядпчдчр