Предмет: Математика,
автор: uyheliy
обчислить значение тригонометрических функций, если tg∝=5, π<∝<
Приложения:
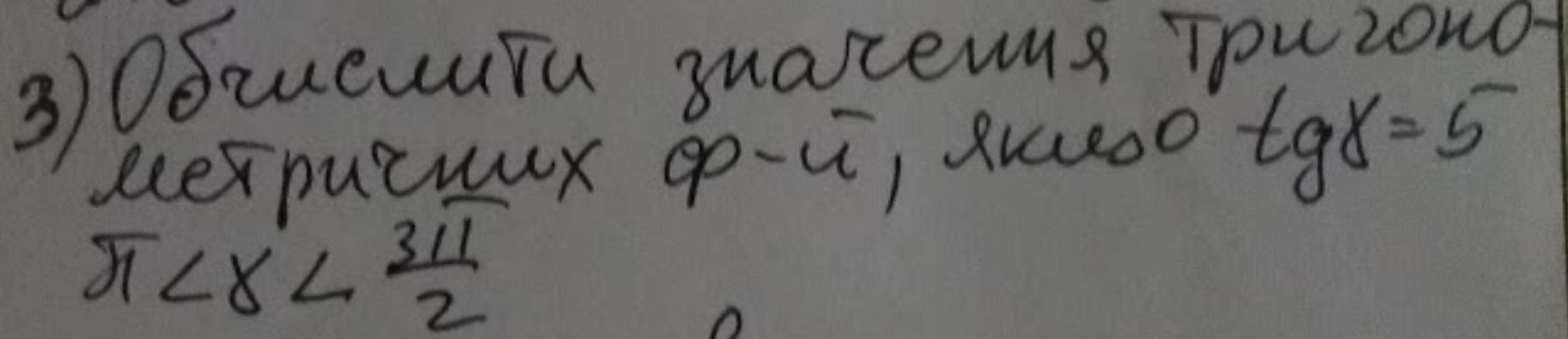
Ответы
Автор ответа:
1
Ответ:
угол принадлежит 3 четверти, синус, косинус отрицательные, котангенс положительный
по формуле:
Похожие вопросы
Предмет: Математика,
автор: 74natali46
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: aleksval6
Предмет: Математика,
автор: luytik12
Предмет: Математика,
автор: Апельсинчик2006