Предмет: Алгебра,
автор: seven23
ДАЮ 40 БАЛЛОВ!
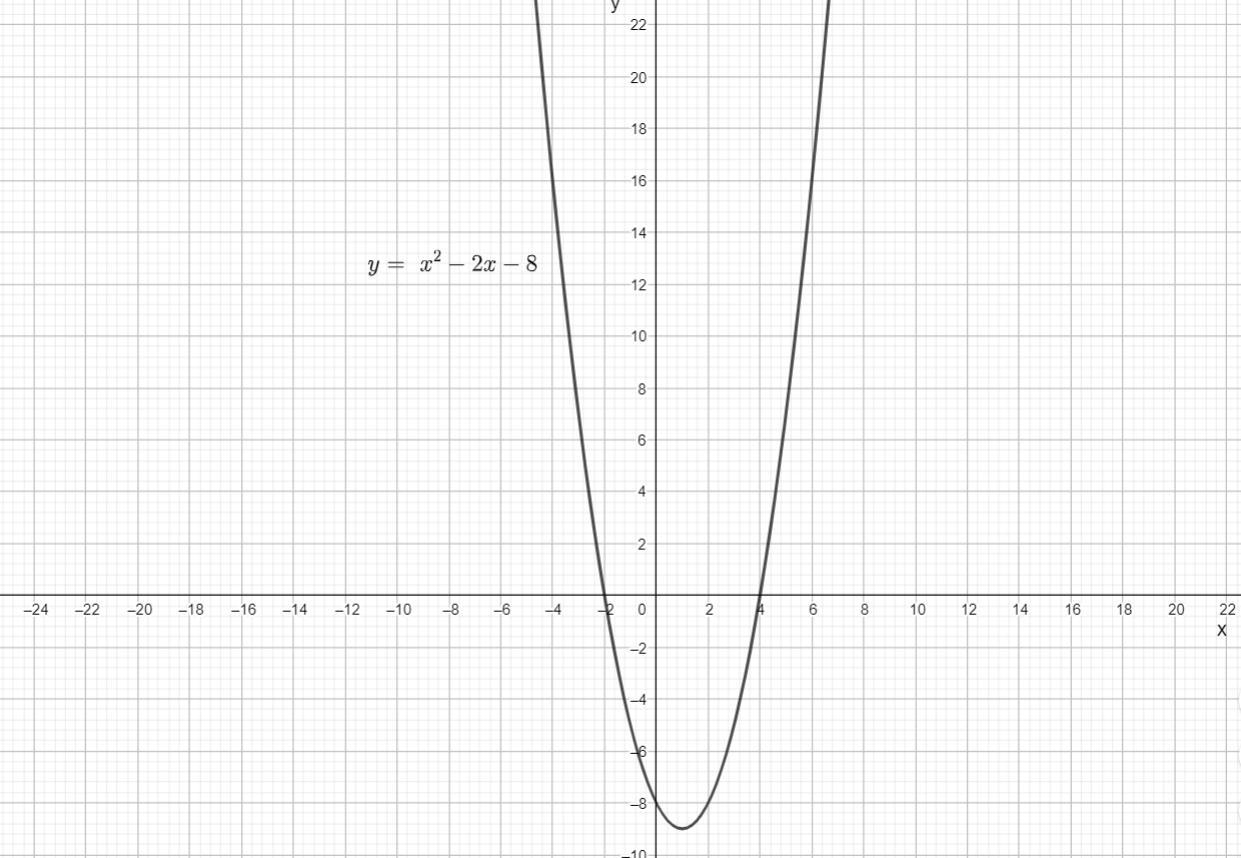
f(x)=x^2-2x-8 используя график функции определите:
1)Область значений функции
2)Промежуток возрастания функции
3)Множество решений неравенства f(x)<0
Ответы
Автор ответа:
4
Объяснение:
Построим график функции. Графиком функции является парабола, ветви которой направлены вверх, найдем координаты вершины параболы
(1; -9) - вершина параболы.
Найдем нули функции, решив уравнение
1) Область значений функции - это множество значений, принимаемых переменной y. По графику можно определить
[ -9; +∞ )
2) Функция возрастает на [ 1; +∞ )
3) Множество значений неравенства можно найти по графику ( множество точек, при которых график функции ниже оси Ох.
x ∈ (-2; 4)
Приложения:
Похожие вопросы
Предмет: Математика,
автор: nikimirzoev20
Предмет: Математика,
автор: парrt
Предмет: Алгебра,
автор: BloodyMark
Предмет: Алгебра,
автор: shslmnsk
Предмет: Физика,
автор: 139vadim88creap0wf8w