Question

Найдите объем куба,если площадь его диагонального сечения равна 2.

Answer 1

Пусть ребро куба равно а.
Диагональ квадрата равна а√2.
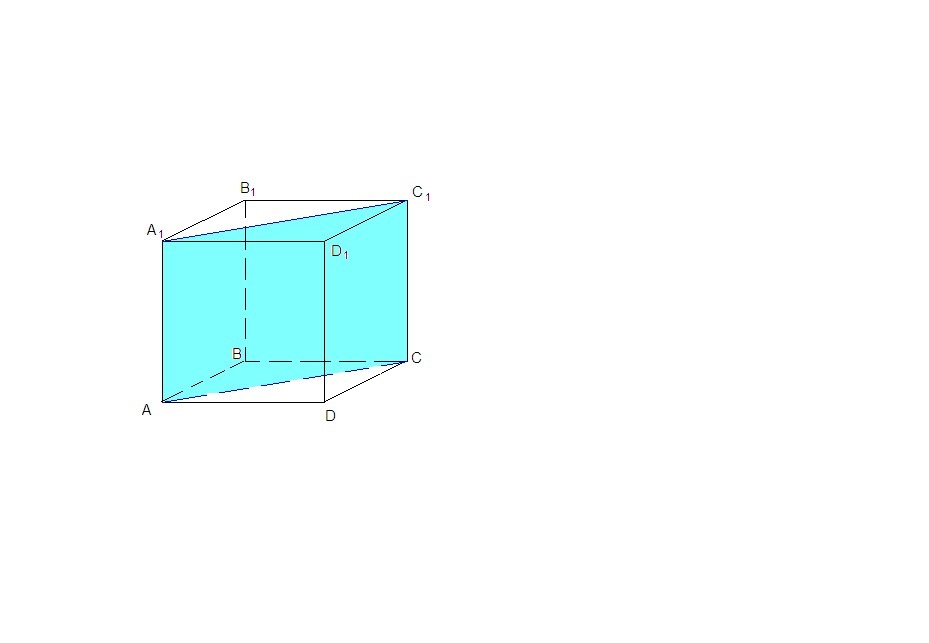
Диагональное сечение куба - прямоугольник, стороны которого равны а и а√2:
a · a√2 = 2
a²√2 = 2
a² = 2/√2
a² = √2
$a= sqrt[4]{2}$

V = a³
$V= ( sqrt[4]{2} )^{3} = sqrt[4]{8}$