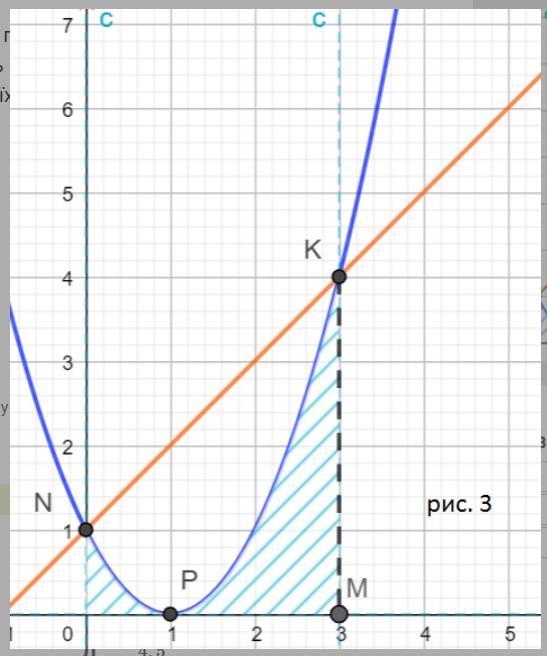
Помогите пожалуйста! Объясните подробно! На рисунке 3 изображены графики функций у = х²-2х + 1 и у = х + 1 . Установите соответствие между криволинейными трапециями (1-3) числовыми значениями их площадей (А-Д)

Ответы
Ответ:
1) Г) 8/3
2) А) 15/2
3) В) 1/3.
Объяснение:
№ 2.
Сначала рассмотрим № 2.
ONKM - это трапеция, основания которой равны 1 и 4, а высота = 3.
Эти размеры мы берём с рисунка.
Площадь трапеции равна произведению полусуммы оснований на высоту:
S onkm = ((1+4):2) · = 2,5 · 3 = 7,5.
Из предложенных ответов подходит А) 15/2 = 7,5.
Ответ: А) 15/2
№ 1 и № 3.
В этих случаях площади можно найти только с использованием определённого интеграла. Определённый интеграл - это площадь фигуры, ограниченной графиком параболы y = х²-2х+1 и заданными пределами интегрирования:
для № 1 - от х=1 до х=3;
для № 3 - от х=0 до х=1.
Сначала находим интеграл от х²-2х+1 (все значения табличные - поэтому не расписываю) - получаем:
х³/3 - х² + х.
Теперь применяем для № 1:
а) считаем (х³/3 - х² + х) при х=3; 27/3 - 9 + 3 = 3;
б) считаем (х³/3 - х² + х) при х=1; 1/3 - 1 + 1 = 1/3;
в) от а) отнимаем б), получаем:
3-1/3= 8/3;
ответ: Г) 8/3;
для № 3:
а) считаем (х³/3 - х² + х) при х=1; 1/3 - 1 + 1 = 1/3;
б) считаем (х³/3 - х² + х) при х=0; 0;
в) от а) отнимаем б):
1/3 - 0 = 1/3;
ответ: В) 1/3.