Предмет: Алгебра,
автор: shevchenkoeg
Пожалуйста, помогите с решением интегралов!
Приложения:
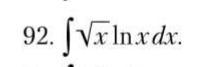
Ответы
Автор ответа:
1
Ответ:
решаем по частям:
по формуле:
ejfkppp12:
помоги пожалуйста с вопросом
Похожие вопросы
Предмет: Физика,
автор: shutkinvikt
Предмет: Математика,
автор: irina30820
Предмет: Русский язык,
автор: P9041032848
Предмет: Литература,
автор: СинийКлён
Предмет: Литература,
автор: larvinyshka