Предмет: Математика,
автор: SashaHutsul
ОЧЕНЬ СРОЧНО! 50 балов!
Вычислить ЛИМИТ
Приложения:
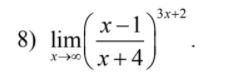
Ответы
Автор ответа:
1
Замена: t = 1/x
Используем эквивалентность бесконечно малой: ln(1+x) = x+o(x)
Ответ: 1/e¹⁵
Похожие вопросы
Предмет: Математика,
автор: GENERAL83
Предмет: Математика,
автор: KaRiNa20043
Предмет: Английский язык,
автор: rudenko12
Предмет: Математика,
автор: Катяумняшка
Предмет: Математика,
автор: Jxjxhdhhxhx