Question

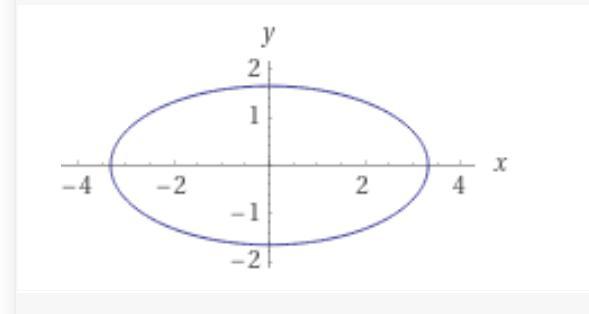
Дан эллипс 4х2 + 16у2 = 44. Найти его полуоси, координаты фокусов, эксцентриситет и уравнения директрис. Изобразить данный эллипс в системе координат

Answer 1

Дан эллипс 4х² + 16у² = 44. Из уравнения видно, что центр его находится в начале координат.

Выразим его уравнение в каноническом виде, разделив обе части на 44:  (4х²/44) + (16у/44) = 44/44.

(х²/11) + (у²/(11/4)) = 1.

Отсюда получаем длины полуосей: a = √11, b = √11/2.

Фокусы находятся на расстоянии "с" от центра.

с = √(a² - b²) = √(11 - (11/4) = √33/2.

Эксцентриситетом эллипса е = с/а = (√33/2)/√11 = √33/(2√11).

Прямые D1:x=−a/e и D2:x=a/e, перпендикулярные главной оси и проходящей на расстоянии a/e от центра, называются директрисами эллипса. D: x = +-(√11)/(√33/(2√11)) = +-(22/√33).