Question

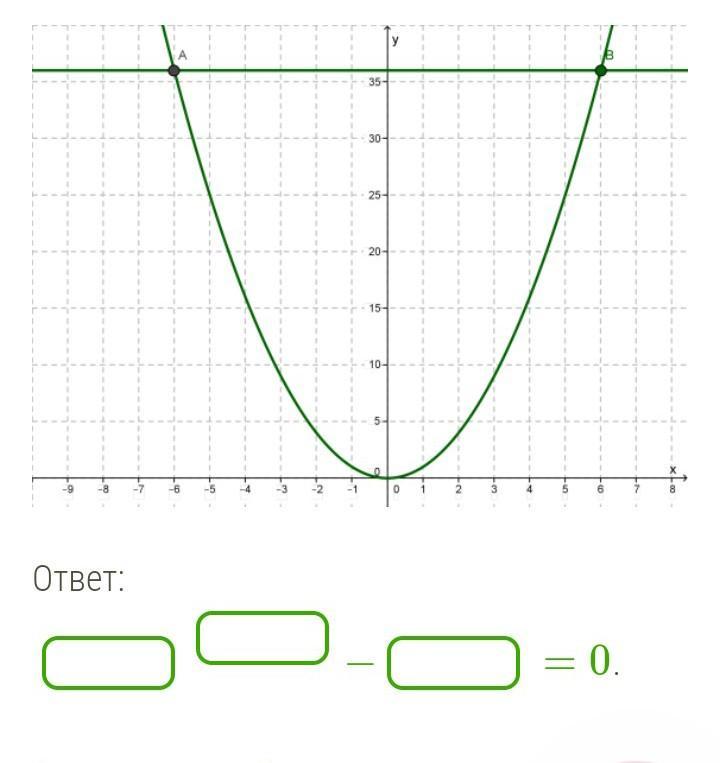
Проанализируй рисунок и запиши квадратное уравнение для нахождения точек пересечения двух графиков функции​

Answer 1

Ответ:

х² - 36 = 0

Пошаговое объяснение:

Прежде всего определим функции по графикам.

Для прямой линии:

поскольку график пересекает ось ОУ в точке (0; 36),  функция будет $y_1=36;$

Для параболы:

это квадратичная функция. Найдем на графике "удобную" точку, т.е. точку, из значения координаты у легко вычислить $\sqrt[2]{}$ , и значение этого корня совпало бы со значением координаты х.

Это точка (5; 25). Тогда функция будет

$y_2=x^2$

Графики функций пересекаются в точке $x_0$, которая является решением уравнения

$y_1=y_2$

Составим это уравнение и получим из него квадратное уравнение нахождения точек пересечения двух графиков функций

$x^2=36 \quad \Rightarrow \quad \underline {\boldsymbol {x^2-36=0}}$ . Это и есть наше решение.

Тогда точки пересечения графиков равны $x_1=6; \quad x2=-6$, что и отражено на графиках.

ответ

квадратное уравнение для нахождения точек пересечения двух графиков функций х² - 36 = 0