Предмет: Алгебра,
автор: 1111111113155
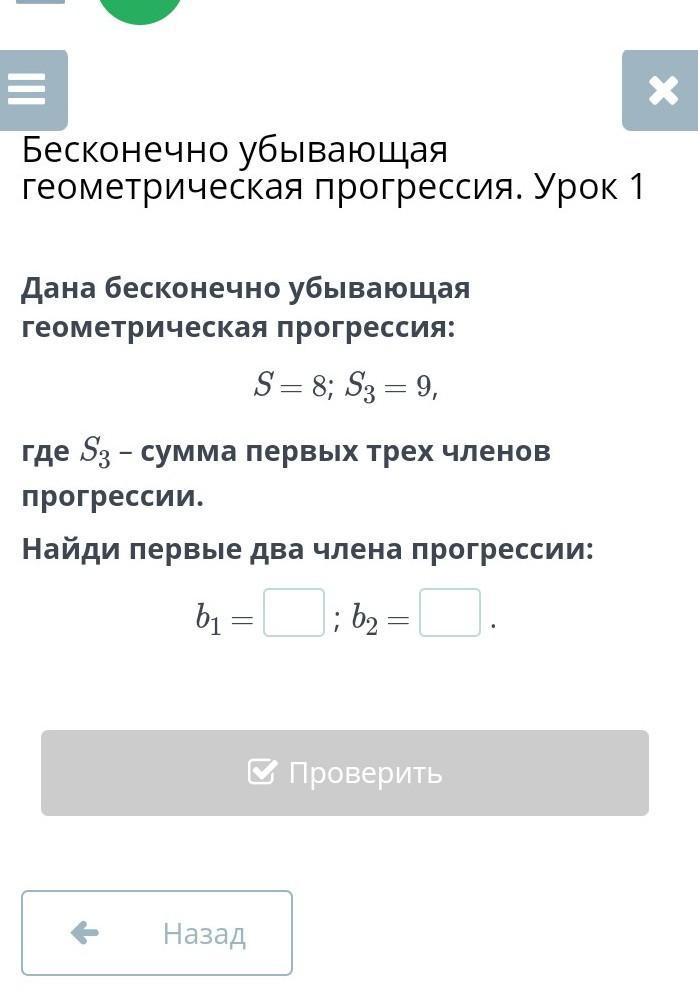
Дана бесконечно убывающая геометрическая прогрессия:
S = 8; S3 = 9,
где S3 – сумма первых трех членов прогрессии.
Найди первые два члена прогрессии:b1 =
; b2 =
помогите
Приложения:
Ответы
Автор ответа:
3
Ответ:
b₁ = 12; b₂ = -6
Объяснение:
Общий вид n-члена геометрической прогрессии имеет вид:
Сумма бесконечной убывающей геометрической прогрессии определяется по формуле
Отсюда
Сумма первых трех членов прогрессии имеет вид
В силу условия
Далее, подставляем выражение b₁ в последнюю формулу:
Определим b₁ и b₂:
Похожие вопросы
Предмет: Химия,
автор: Dima20051999
Предмет: Биология,
автор: liana197505
Предмет: Математика,
автор: Аноним
Предмет: Литература,
автор: bodaginaylo33