Question

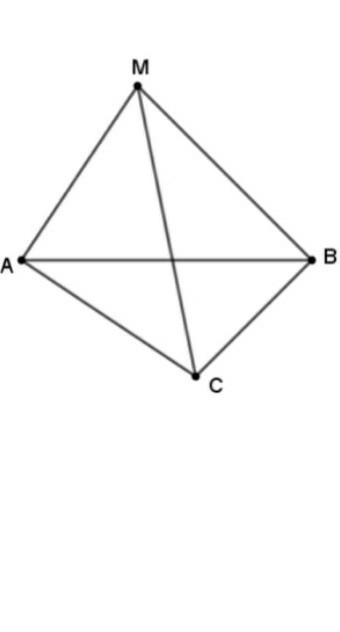
Точка M находится вне плоскости треугольника ABC (рис.). Треугольники ∆ABC ∆MAB, ∆MBC, ∆MAC равносторонние. Найдите угол между плоскостями треугольников ∆ABCи ∆MAC.​

Answer 1

Ответ:

$\alpha =arccos\dfrac{1}{3}$

Объяснение:

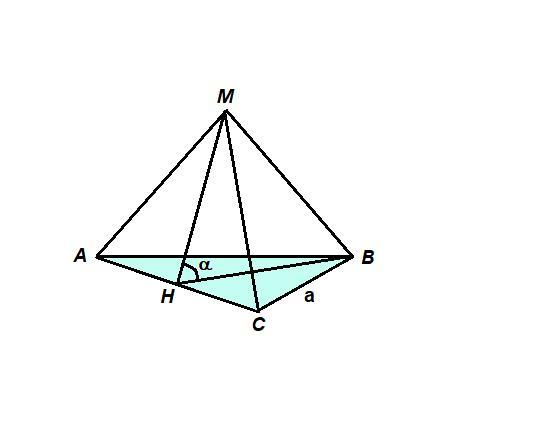
Пусть Н - середина АС.

Тогда ВН⊥АС как медиана и высота равностороннего треугольника АВС,

МН⊥АС как медиана и высота равностороннего треугольника МАС,

⇒ ∠МНВ - линейный угол двугранного угла между плоскостями треугольников АВС и МАС.

Если стороны треугольников равны а, то по формуле высоты равностороннего треугольника:

$MH=BH=\dfrac{a\sqrt{3}}{2}$

Из ΔМНВ по теореме косинусов:

$MB^2=MH^2+BH^2-2MH\cdot BH\cdot \cos\alpha$

$a^2=\dfrac{3a^2}{4}+\dfrac{3a^2}{4}-2\cdot \dfrac{3a^2}{4}\cdot \cos \alpha$

$a^2=\dfrac{3a^2}{2}-\dfrac{3a^2}{2}\cdot \cos\alpha$

$\cos \alpha=\dfrac{\dfrac{3a^2}{2}-a^2}{\dfrac{3a^2}{2}}=\dfrac{a^2}{2}\cdot \dfrac{2}{3a^2}=\dfrac{1}{3}$

$\alpha =arccos\dfrac{1}{3}$