Предмет: Математика,
автор: vikamelichova
ПОМОГИТЕ, ПОЖАЛУЙСТА, РЕШИТЬ ИНТЕГРАЛЫ. ОЧЕНЬ НАДО
Приложения:
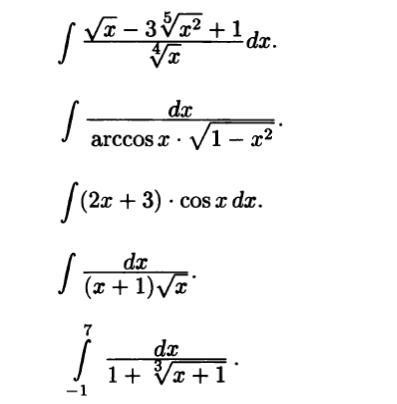
Ответы
Автор ответа:
0
Ответ:
2)
Замена:
3) По частям:
По формуле:
4)
Замена:
5)
Замена:
Подставляем пределы (2 и 0)
Похожие вопросы
Предмет: Русский язык,
автор: vladdyatlov
Предмет: География,
автор: Katemantis
Предмет: Русский язык,
автор: ava3
Предмет: Биология,
автор: virstyuk81