Question

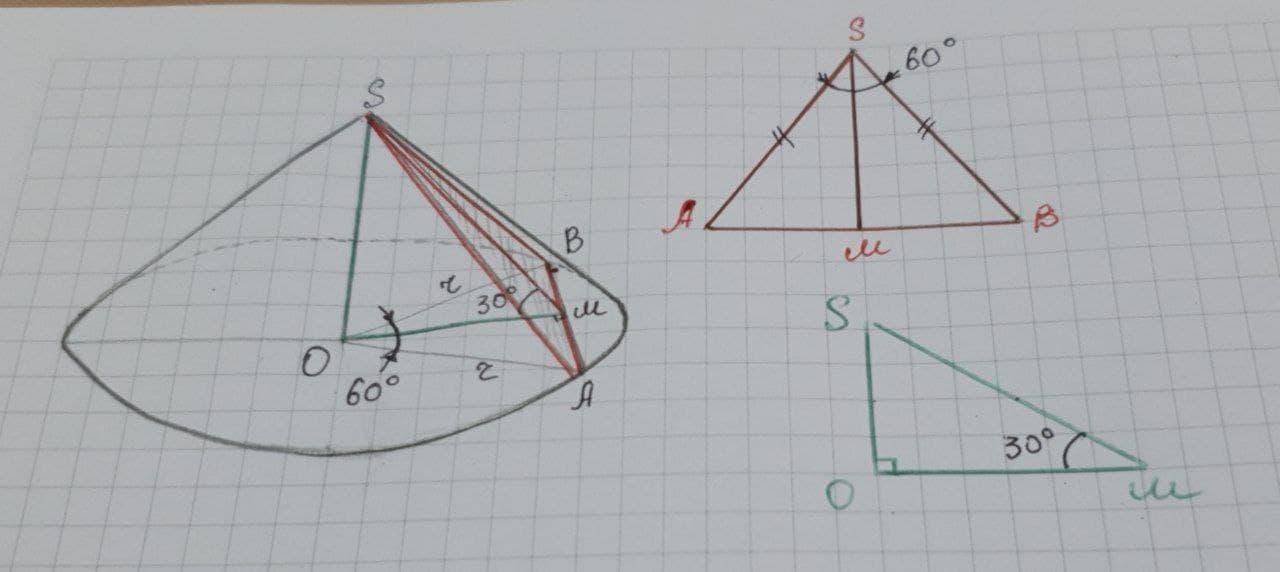
Радіус основи конуса дорівнює r. Визначити площу перерізу, який проходить через вершину конуса і хорду основи, яка стягує дугу в 60 градусів, якщо площина перерізу утворює з площиною основи конуса кут 30 градусів.Дам
55 балів!!!

Answer 1

Ответ:

r²/2

Объяснение:

(ASB) - переріз, який проходить через вершину конуса і хорду основи, яка стягує дугу в 60°.

S ΔASB - ?

1.  ΔAOB - рівнобедрений: ОА=ОВ= r, AB – хорда.

∠AOB=60°(за умовою) - центральний кут вписаним у круг, що опирається на відповідну дугу. За  властивістю про рівність кутів при основі рівнобедреного ΔAOB маємо:  

∠OAB=∠OBA=∠AOB=60°.

⇒ΔAOB - рівносторонній  тому AB=AO=OB=r.

Проведемо ОМ⊥АВ, OM - висота, ⇒ OM– медіана і бісектриса рівнобедреного ΔAOB (за властивістю).

⇒AM=BM=AB/2=r/2, ∠AOM=∠AOB/2=60°/2=30°

2. ΔAMО (∠AMO=90°)

OM=AO*cos ∠AOM= r * $\frac{\sqrt{3} }{2}$

3.  ΔSOM (∠SOM=90°)

∠SMO=30° – кут між перерізом (ΔASB) і площиною основи конуса.

SM = OM / cos ∠SMO = ( r * $\frac{\sqrt{3} }{2}$  ) / $\frac{\sqrt{3} }{2}$ = r

4. ΔASB

SO⊥OM, OM⊥AB ⇒ за теоремою «про три перпендикуляри» SM⊥AB

SM - висота ΔASB.

S ΔASB = $\frac{1}{2}$ * AB * SM =  $\frac{1}{2}$ * r * r =  $\frac{1}{2}$ * r²