Question

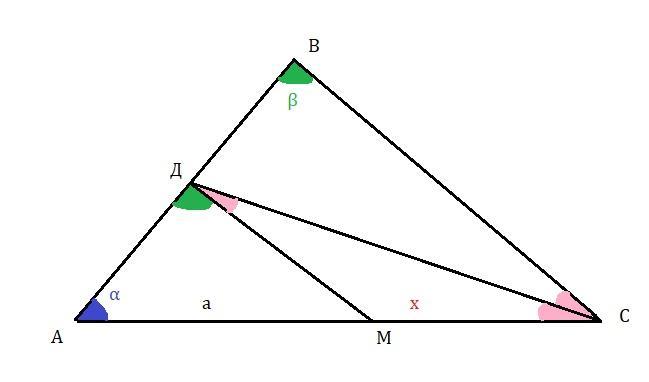
Дан треугольник ABC, в котором ∠A = α, ∠B = β. На стороне AB взята точка D, а на стороне AC – точка M, причём CD – биссектриса треугольника ABC,
DM || BC и AM = a. Найдите CM.

​

Answer 1

Объяснение:

ДМ║ВС, ДС - секущая ⇒ ∠ВСД=∠МДС - как внутренние накрест лежащие углы, но ∠ВСД = ∠МСД, т.к. СД - биссектриса ⇒

∠МДС=∠МСД.

Это  углы при основании ДС треугольника ΔДСМ ⇒ этот треугольник равнобедренный: ДМ=СМ=х

Рассмотрим ΔАДМ.

∠АДМ = ∠АВС = β - как внутренние односторонние углы при параллельных прямых ДМ и ВС и секущей АВ

По теореме синусов имеем:

$\frac{a}{sin <ADM} =\frac{DM}{sin <DAM}$

$\frac{a}{sin \beta } = \frac{x}{sin \alpha }$

$x=\frac{asin\alpha }{sin\beta }$

Т.к. СМ=ДМ, то СМ= а* sinα / sinβ